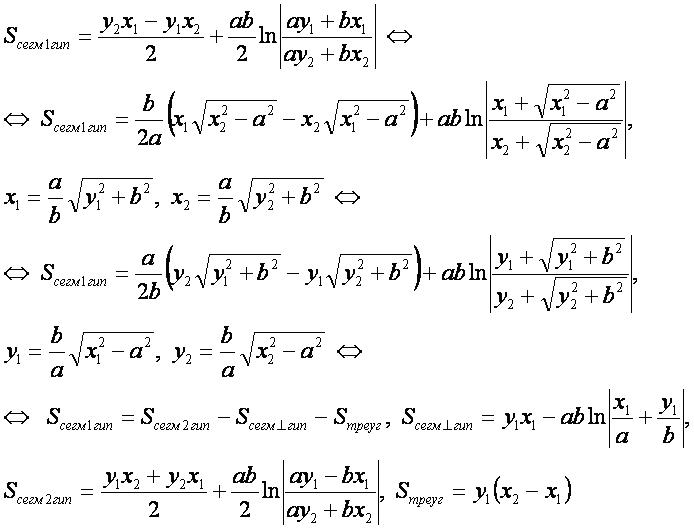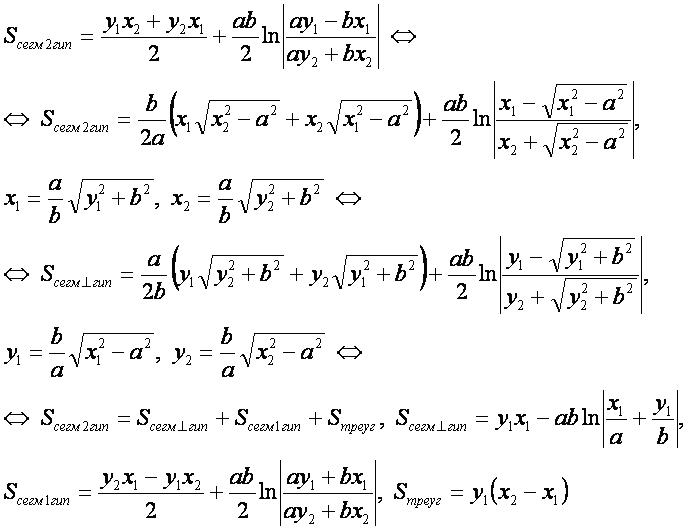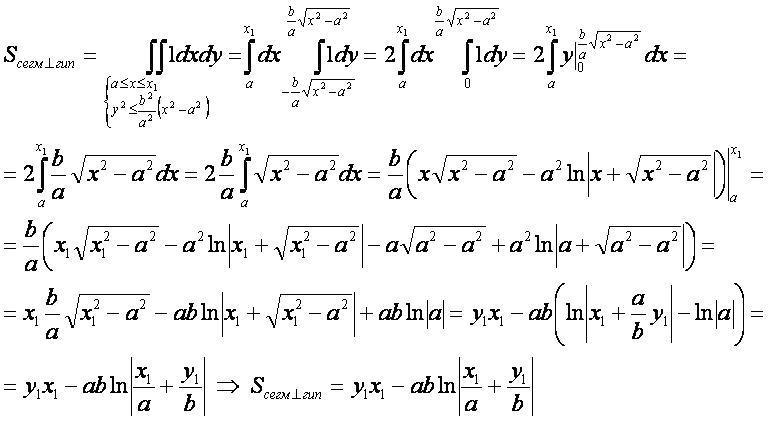Площадь сегмента гиперболы
Версия от 13:38, 10 февраля 2021; Logic-samara (обсуждение | вклад)
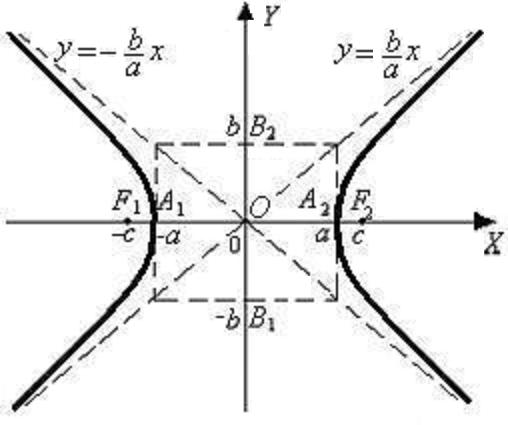
Площадь сегмента гиперболы — это число, характеризующее сегмент гиперболы в единицах измерения площади.
Сегмент гиперболы — это конечная фигура, отсекаемая прямой от гиперболы.
Виды сегментов:
- перпендикулярный оси гиперболы;
- отсекаемый от одной ветви гиперболы;
- отсекаемый от двух ветвей гиперболы.
Обозначения
Введём обозначения:
x1 — абсцисса первой крайней точки сегмента;
y1 — ордината первой крайней точки сегмента;
x2 — абсцисса второй крайней точки сегмента;
y2 — ордината второй крайней точки сегмента;
Sтреуг — площадь треугольника;
Sсегм.гип — площадь сегмента гиперболы.
Формулы:
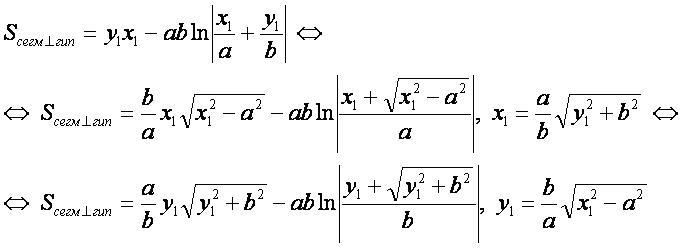
Площадь сегмента, перпендикулярного оси гиперболы
Площадь сегмента, отсекаемого от одной ветви гиперболы
Площадь сегмента, отсекаемого от двух ветвей гиперболы
Вывод формул:
Площадь сегмента, перпендикулярного оси гиперболы
- Для вывода используется формула "площадь плоской фигуры" в прямоугольных координатах.
Площадь сегмента, отсекаемого от одной ветви гиперболы
- Для вывода используется формула "площадь плоской фигуры" в прямоугольных координатах.
Площадь сегмента, отсекаемого от двух ветвей гиперболы
- Для вывода используется формула "площадь плоской фигуры" в прямоугольных координатах.
Другие фигуры:
- плоская фигура;
- круг;
- сегмент круга;
- сектор круга;
- сегмент правильного многоугольника;
- сектор правильного многоугольника;
- серп;
- сегмент параболы;
- эллипс;
- сегмент эллипса;
- сектор эллипса;
- серп эллипса;
- сегмент гиперболы;
- арка синусоиды;
- арка косинусоиды;
- фигура, ограниченная тангенсоидой и осью абсцисс;
- фигура, ограниченная котангенсоидой и осью абсцисс;
- арка циклоиды;
- сектор кардиоиды;
- фигура, ограниченная цепной линией и осью абсцисс;
- фигура, ограниченная трактрисой и осью абсцисс;
- сектор лемнискаты Бернулли.