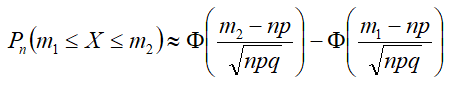Интегральная теорема Лапласа

Интегральная теорема Лапласа — интегральная теорема, предложенная Лапласом.

Если при каждом из независимых испытаний вероятность появления некоторого случайного события постоянна, то вероятность появления события фиксированное число раз подчинена биномиальному закону, а при достаточно большом числе испытаний биномиальный закон асимптотически приближается к нормальному закону, поэтому вероятность появления события не менее фиксированного числа раз и не более другого фиксированного числа приближённо равна разности значений интегральной функции Лапласа от центрированных и стандартизованных фиксированных значений.

Обозначения

X — число появлений случайного события;

p — вероятность появления случайного события;

q — вероятность противоположного события, причём q=1-p;

n — число испытаний;

m — граница числа появлений события X;

np — средняя — математическое ожидание числа появлений события X;

npq — дисперсия числа появлений события X;

m₁ — нижняя граница диапазона;

m₂ — верхняя граница диапазона;

P_n(m₁≤X≤m₂) — вероятность появлений события X не менее m₁ и не более m₂ раз при n испытаниях;

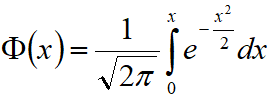— интегральная функция Лапласа, отличается от интегральной функции нормального закона для стандартизованной случайной величины на 0,5, т.е. F(x)=Ф(x)+0,5.