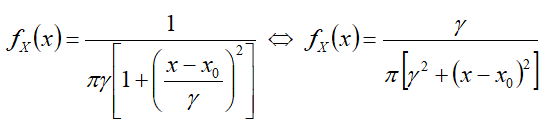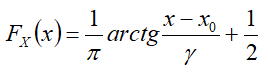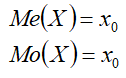Распределение Коши
Распределение Коши — это распределение случайной величины.
Распределением Коши характеризуется длина отрезка, отсекаемого на оси абсцисс прямой, закреплённой в точке на оси ординат, если угол между прямой и осью ординат имеет равномерное распределение на интервале (−π; π).
Случайная величина, имеющая распределение Коши, не имеет математического ожидания и дисперсии.
Содержание
Обозначения
X — случайная величина;
x0 — параметр сдвига, -∞<x0<+∞;
γ — параметр масштаба, γ>0;
fX(x) — дифференциальная функция распределения — функция плотности вероятности;
FX(x) — интегральная функция распределения — функция вероятности;
Me(X) — медиана;
Mo(X) — мода.
Функции распределения:
Дифференциальная функция
Формулы
Графики
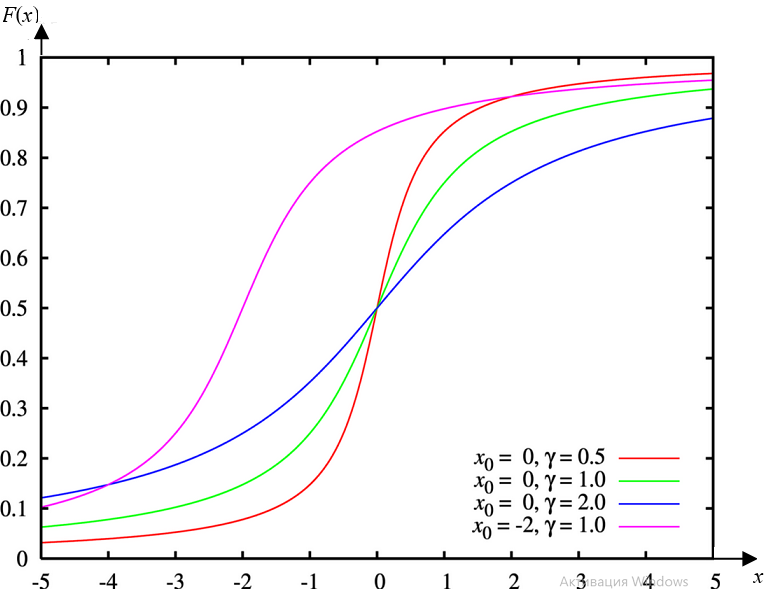
- При x0=0 и γ=1 распределение Коши называется Стандартное распределение Коши.
Интегральная функция
Формулы
Графики
Характеристики:
Другие распределения:
Распределения ДСВ:
- распределение Бернулли;
- биномиальное распределение;
- геометрическое распределение;
- гипергеометрическое распределение;
- дискретное равномерное распределение;
- распределение Пуассона;
Распределения НСВ:
- бета-распределение;
- распределение Вейбулла;
- гамма-распределение;
- квадратичное распределение;
- распределение Коши;
- распределение Лапласа;
- линейное распределение;
- логистическое распределение;
- логнормальное распределение;
- нормальное распределение;
- распределение Парето;
- показательное распределение;
- равномерное распределение;
- распределение Рэлея;
- распределение Сосновского;
- распределение Стьюдента;
- распределение Фишера-Снедекора;
- распределение Хи-квадрат;
- экспоненциальное распределение;
- Эль-распределение.
Ссылки
- Википедия. Распределение Коши.
- https://ru.wikipedia.org/wiki/Распределение_Коши
- Участник:Logic-samara