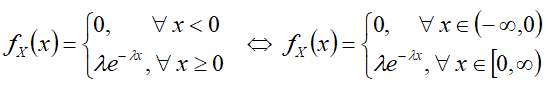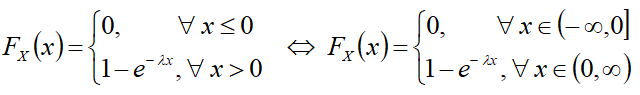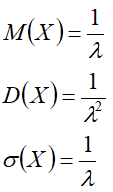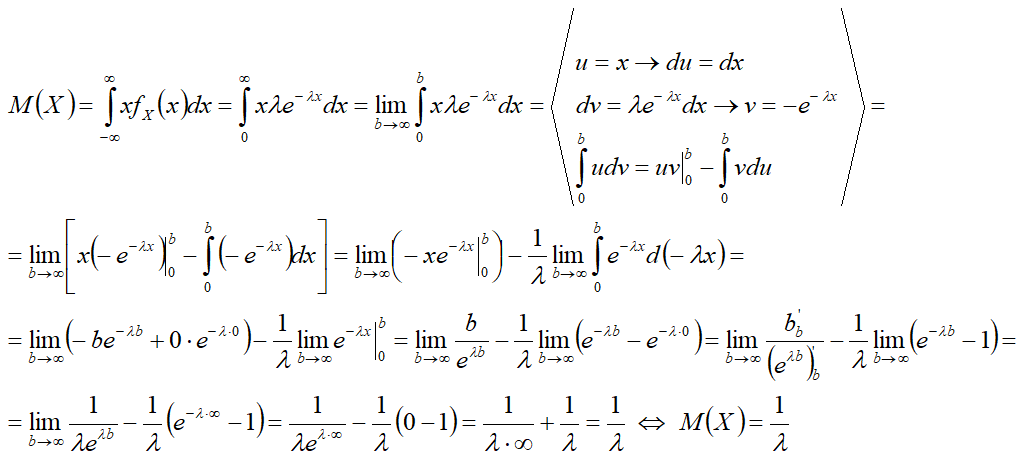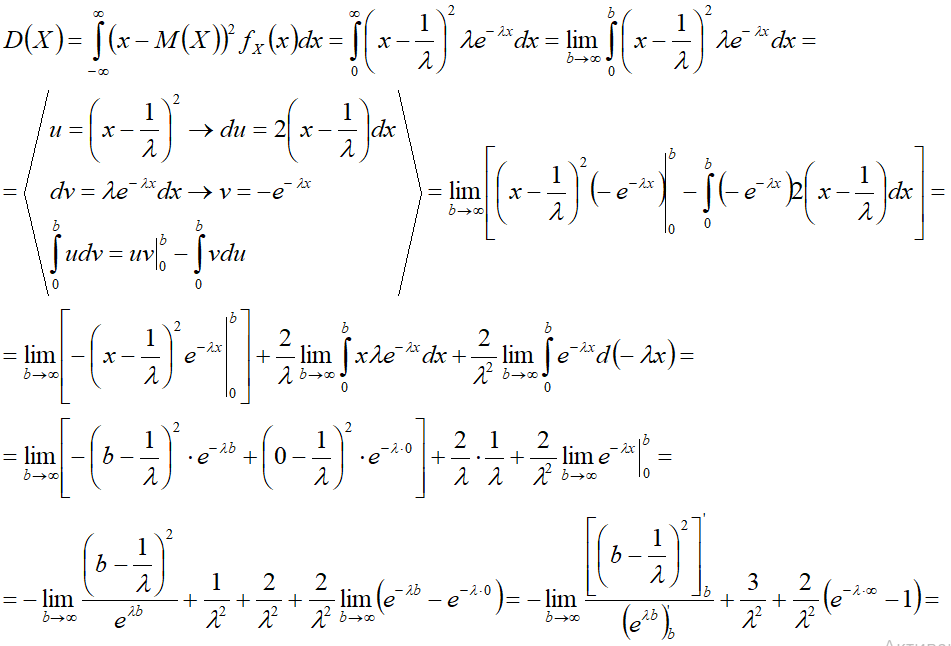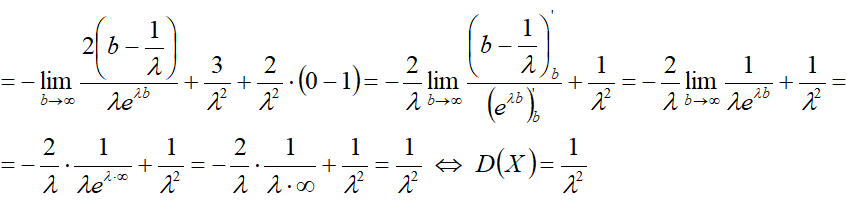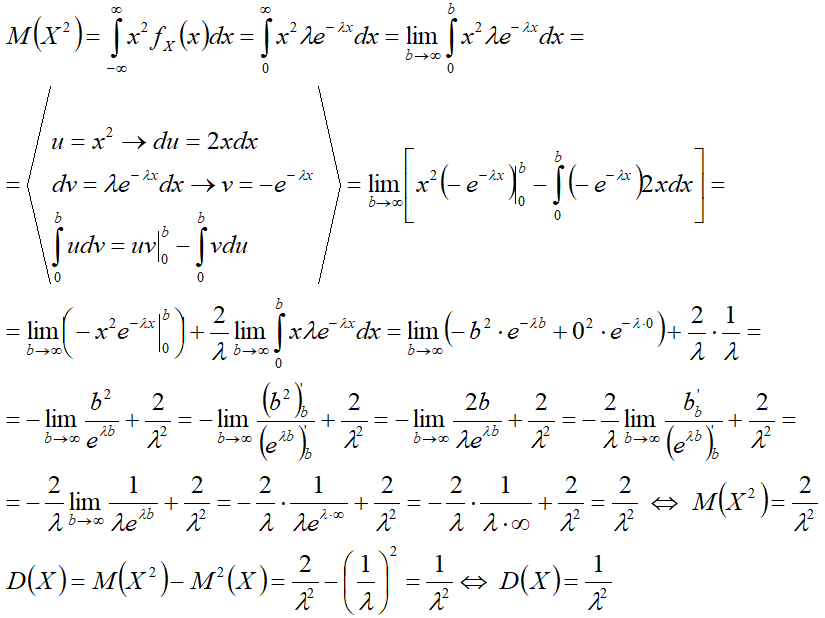Экспоненциальное распределение
Экспоненциальное распределение (показательное распределение) — это распределение непрерывной случайной величины, равной интервалу времени между двумя любыми соседними событиями в простейшем потоке с интенсивностью λ.
В функциях экспоненциального распределения есть экспонента e-λx.
Содержание
Обозначения
X — случайная величина;
fX(x) — дифференциальная функция распределения — функция плотности вероятности;
FX(x) — интегральная функция распределения — функция вероятности;
λ — интенсивность простейшего потока;
M(X) — средняя — математическое ожидание;
D(X) — дисперсия;
σ(X) — среднеквадратическое отклонение;
Me(X) — медиана;
Mo(X) — мода;
As(X) — коэффициент асимметрии;
Ek(X) — коэффициент эксцесса.
Функции распределения:
Дифференциальная функция
Формулы
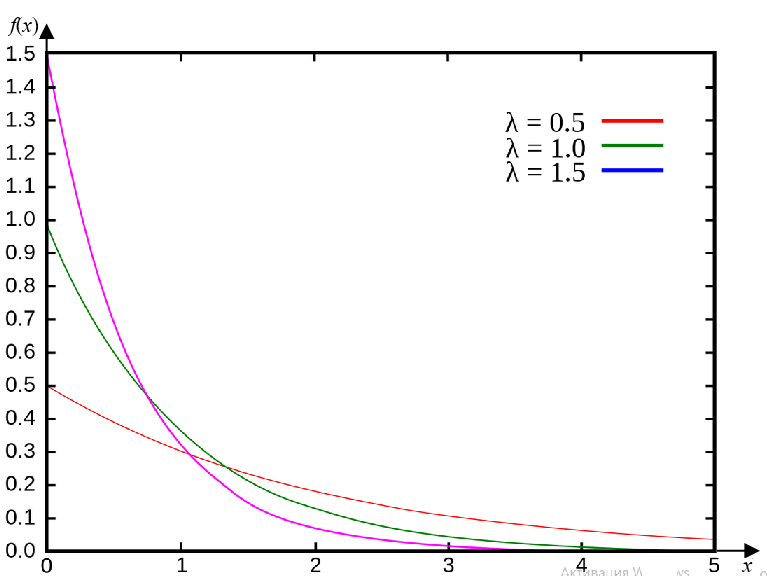
Графики
Интегральная функция
Формулы
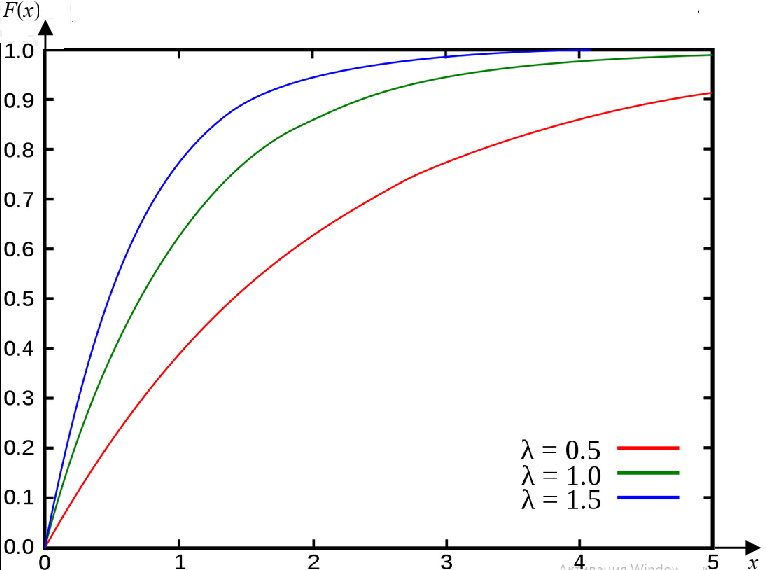
Графики
Характеристики:
Вывод формул:
Математическое ожидание
Дисперсия
1-й способ
2-й способ
Другие распределения:
Распределения ДСВ:
- распределение Бернулли;
- биномиальное распределение;
- геометрическое распределение;
- гипергеометрическое распределение;
- дискретное равномерное распределение;
- распределение Пуассона;
Распределения НСВ:
- бета-распределение;
- распределение Вейбулла;
- гамма-распределение;
- квадратичное распределение;
- распределение Коши;
- распределение Лапласа;
- линейное распределение;
- логистическое распределение;
- логнормальное распределение;
- нормальное распределение;
- распределение Парето;
- показательное распределение;
- равномерное распределение;
- распределение Рэлея;
- распределение Сосновского;
- распределение Стьюдента;
- распределение Фишера-Снедекора;
- распределение Хи-квадрат;
- экспоненциальное распределение;
- Эль-распределение.
Ссылки
- Овчаров Л. А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969, стр.18.
- Википедия. Экспоненциальное распределение.
- https://ru.wikipedia.org/wiki/Экспоненциальное_распределение
- Участник:Logic-samara