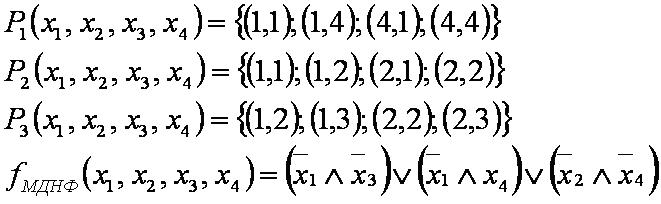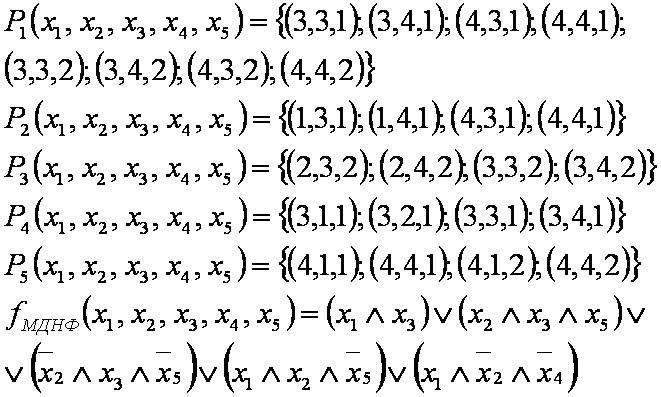Минимальная дизъюнктивная нормальная форма
Минимальная дизъюнктивная нормальная форма (МДНФ) для логической функции – это дизъюнкция с минимальным числом элементарных конъюнкций с минимальным числом аргументов (либо самих, либо их отрицаний) данной функции. При этом таблицы истинности для логической функции и её МДНФ совпадают.
Минимальная дизъюнктивная нормальная форма для логической функции с числом аргументов до четырёх может быть построена с помощью карт Карно. Для этого единицы карты Карно последовательно покрываются прямоугольниками 4х2, 2х4, 2х2, 4х1, 1х4, 2х1, 1х2 и 1х1. Затем строятся элементарные конъюнкты МДНФ.
Содержание
Формула
Введём обозначения:
n – число аргументов функции;
k – число прямоугольников на карте Карно;
(x1,x2,…,xn) – набор аргументов функции;
f(x1,x2,…,xn) – логическая функция;
Pt(x1,x2,…,xn)={(i1,l1); (i2,l2); ...; (im,lm)} – множество клеток t-прямоугольника;
Pt(x1,x2,…,xn)=1 – множество клеток t-прямоугольника из единиц;
argj(i,l) – значение аргумента xj в наборе аргументов для клетки (i,l);
fМДНФ(x1,x2,…,xn) – МДНФ логической функции.
Примеры построения МДНФ
Пример 1
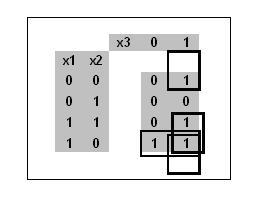
Строим карту Карно для функции трёх переменных
Единицы карты Карно минимально покрываются одним прямоугольником вида 1х2 и двумя прямоугольниками вида 2х1, что соответствует трём элементарным конъюнкциям двух аргументов. Заметим, что два неполных прямоугольника вида 2х1 соответствуют одному полному прямоугольнику покрытия.
Пример 2
Строим карту Карно для функции четырёх переменных
Единицы карты Карно минимально покрываются тремя квадратами вида 2х2, что соответствует трём элементарным конъюнкциям двух аргументов. Заметим, что четыре угловых неполных квадрата соответствуют одному полному квадрату покрытия.
Пример 3
Строим трёхмерную карту Карно для функции пяти переменных
Единицы трёхмерной карты Карно минимально покрываются параллелепипедами вида 2х2х2, 2х2х1 (два), 1х4х1, 1х2х2, что соответствует одной элементарной конъюнкции двух аргументов и четырём элементарным конъюнкциям трёх аргументов. Заметим, что крайние по сторонам и угловые фигуры объединяются.
