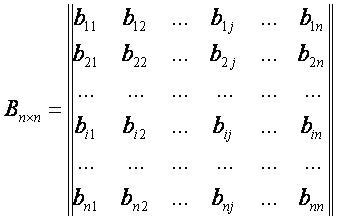Обратная матрица — различия между версиями
м |
м |
||
| Строка 13: | Строка 13: | ||
'''Δ''' – [[определитель]] матрицы; | '''Δ''' – [[определитель]] матрицы; | ||
| − | [[файл:МАТ10.JPG]] – матрица | + | [[файл:МАТ10.JPG]] – исходная матрица; |
| − | [[файл:МАТ20.JPG]] – матрица | + | [[файл:МАТ20.JPG]] – обратная матрица; |
| − | [[файл:МАТ00.JPG]] – единичная матрица | + | [[файл:МАТ00.JPG]] – единичная матрица. |
== Формула == | == Формула == | ||
[[файл:ОБМ01.JPG]] | [[файл:ОБМ01.JPG]] | ||
| + | *Обратная матрица существует, если определитель исходной матрицы равен нулю. | ||
*Заметим, что обратная матрица не существует, если определитель исходной матрицы равен нулю. | *Заметим, что обратная матрица не существует, если определитель исходной матрицы равен нулю. | ||
| + | *Обратная матрица для единичной тоже единичная. | ||
== Свойства: == | == Свойства: == | ||
[[файл:ОБМ02.JPG]] | [[файл:ОБМ02.JPG]] | ||
Текущая версия на 18:01, 23 октября 2024
Обратная матрица – это такая матрица, которая при умножении на исходную и наоброт, при умножении на которую исходной, получается единичная матрица.
Содержание
Обозначения[править]
n – порядок матрицы;
nxn – размерность матрицы;
aij – элемент матрицы, лежащий на пересечении i-ой строки и j-ого столбца матрицы A;
bij – элемент матрицы, лежащий на пересечении i-ой строки и j-ого столбца матрицы B;
Aij – алгебраическое дополнение элемента aij матрицы A;
Δ – определитель матрицы;
Формула[править]
- Обратная матрица существует, если определитель исходной матрицы равен нулю.
- Заметим, что обратная матрица не существует, если определитель исходной матрицы равен нулю.
- Обратная матрица для единичной тоже единичная.
Свойства:[править]
- Заметим, что определитель обратной матрицы равен обратной величине определителя исходной матрицы.
Другие операции:[править]
- сложение матриц;
- вычитание матриц;
- умножение матрицы на число;
- умножение матриц;
- умножение элементов матриц;
- деление элементов матриц;
- возведение в квадрат элементов матрицы;
- извлечение корня из элементов матрицы;
- деление матриц;
- транспонирование матрицы;
- обращение матрицы;
- обращение клеточной матрицы;
- возведение в степень матрицы;
- нахождение определителя;
- нахождение минора;
- нахождение алгебраического дополнения.