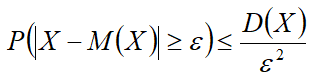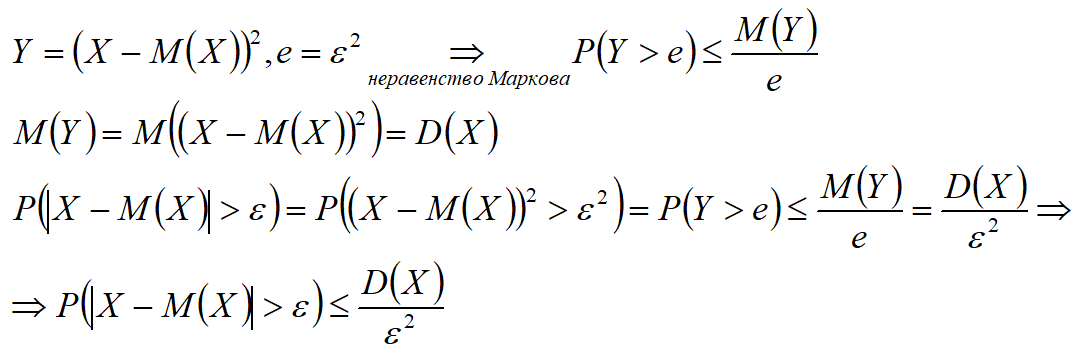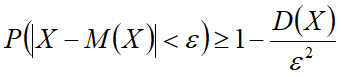Неравенство Чебышёва — различия между версиями
м |
м |
||
| Строка 1: | Строка 1: | ||
[[Вероятность]] того, что модуль отклонения случайной величины от её математического ожидания превысит некоторое положительное число, не более отношения [[Дисперсия непрерывной случайной величины|дисперсии]] этой случайной величины к квадрату заданного числа. | [[Вероятность]] того, что модуль отклонения случайной величины от её математического ожидания превысит некоторое положительное число, не более отношения [[Дисперсия непрерывной случайной величины|дисперсии]] этой случайной величины к квадрату заданного числа. | ||
== Обозначения == | == Обозначения == | ||
| − | '''X''' – | + | '''X''' – случайная величина; |
'''M(X)''' – математическое ожидание случайной величины '''X'''; | '''M(X)''' – математическое ожидание случайной величины '''X'''; | ||
| Строка 9: | Строка 9: | ||
'''ε''' – положительное число большее чем корень из '''D(X)'''; | '''ε''' – положительное число большее чем корень из '''D(X)'''; | ||
| − | '''Y''' — положительная | + | '''Y''' — положительная случайная величина; |
'''M(Y)''' — математическое ожидание случайной величины '''Y'''; | '''M(Y)''' — математическое ожидание случайной величины '''Y'''; | ||
| Строка 16: | Строка 16: | ||
== Формула неравенства == | == Формула неравенства == | ||
[[файл:НЧ01.png]] | [[файл:НЧ01.png]] | ||
| − | *Заметим, что [[вероятность]] равенства для [[Характеристики непрерывной случайной величины|непрерывной случайной величины]] равна нулю, поэтому строгое и нестрогое неравенства событий равнозначны. | + | *Заметим, что [[вероятность]] равенства для [[Характеристики непрерывной случайной величины|непрерывной случайной величины (НСВ)]] равна нулю, поэтому строгое и нестрогое неравенства событий равнозначны. |
== Доказательство для НСВ == | == Доказательство для НСВ == | ||
[[файл:НЧ20.png]] | [[файл:НЧ20.png]] | ||
Версия 12:06, 7 февраля 2025
Вероятность того, что модуль отклонения случайной величины от её математического ожидания превысит некоторое положительное число, не более отношения дисперсии этой случайной величины к квадрату заданного числа.
Содержание
Обозначения
X – случайная величина;
M(X) – математическое ожидание случайной величины X;
D(X) – дисперсия случайной величины X;
ε – положительное число большее чем корень из D(X);
Y — положительная случайная величина;
M(Y) — математическое ожидание случайной величины Y;
e — положительное число большее чем M(Y).
Формула неравенства
- Заметим, что вероятность равенства для непрерывной случайной величины (НСВ) равна нулю, поэтому строгое и нестрогое неравенства событий равнозначны.
Доказательство для НСВ
Следствие
Другие неравенства:
- неравенство n-степени числа;
- неравенство Йенсена;
- неравенство Коши;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
Ссылки
- Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2004, стр.225.
