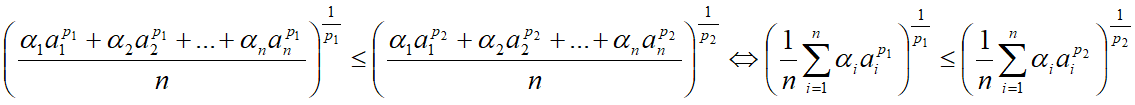Неравенство взвешенных p-ичных средних — различия между версиями
(начало) |
м |
||
| Строка 3: | Строка 3: | ||
'''n''' – число положительных чисел; | '''n''' – число положительных чисел; | ||
| − | '''p<sub>1</sub>''' – степень | + | '''p<sub>1</sub>''' – меньшая степень p-ичной средней; |
| − | '''p<sub>2</sub>''' – степень | + | '''p<sub>2</sub>''' – большая степень p-ичной средней; |
'''a<sub>i</sub>''' – '''i'''-ое положительное число; | '''a<sub>i</sub>''' – '''i'''-ое положительное число; | ||
Версия 17:06, 13 февраля 2025
Для отличных от нуля действительных p из двух взвешенных p-ичных средних положительных чисел, средняя для меньшего p не больше средней для большего p.
Обозначения
n – число положительных чисел;
p1 – меньшая степень p-ичной средней;
p2 – большая степень p-ичной средней;
ai – i-ое положительное число;
αi – i-ый удельный вес;
α1+α2+…+αn=1 – сумма удельных весов.
Формула неравенства
Другие неравенства:
- неравенство n-степени числа;
- неравенство Йенсена;
- неравенство Коши;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
