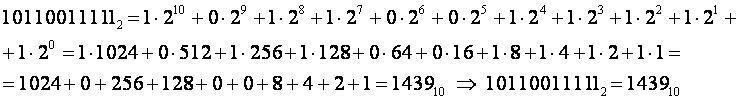Система счисления

Система счисления — это система записи чисел с помощью цифр, причём положение цифры в числе определяет её вес и численное значение.

Система счисления полностью определяется основанием – числом, которое определяет число цифр (начиная с цифры ноль) в системе и степени которого (начиная с нулевой) определяют веса разрядов чисел (справа налево).

Примеры систем счисления:

• двоичная (цифры:0-1);
• троичная (цифры:0-2);
• четверичная (цифры:0-3);
• пятеричная (цифры:0-4);
• шестеричная (цифры:0-5);
• семеричная (цифры:0-6);
• восьмеричная (цифры:0-7);
• девятеричная (цифры:0-8);
• десятичная (цифры:0-9);
• одиннадцатиричная (цифры:0-9,A);
• двенадцатеричная (цифры:0-9,A-B);
• тринадцатеричная (цифры:0-9,A-C);
• четырнадцатеричная (цифры:0-9,A-D);
• пятнадцатеричная (цифры:0-9,A-E);
• шестнадцатеричная (цифры:0-9,A-F).

Для перевода чисел из одной системы счисления в другую используются алгоритмы перевода чисел.

Примеры алгоритмов:

Перевод чисел из десятичной системы счисления

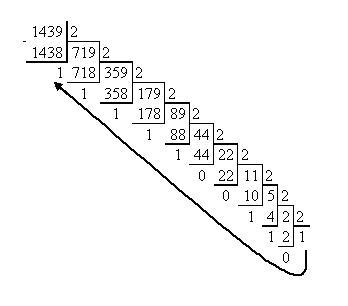
Сначала производится последовательное деление столбиком исходного числа и получаемых (от предыдущих делений) частных (больших или равных основанию) на основание новой системы счисления и записываются остатки от делений. Деление продолжается до тех пор, пока частное не станет меньше основания. Затем выписываются цифры в новой системе счисления вместо (полученных в десятичной системе счисления) последнего частного и остатков от делений в обратном (получению) порядке. Полученное число является записью исходного числа в новой системе счисления.

Пример перевода 10→2

1439₁₀=10110011111₂

Перевод чисел в десятичную систему счисления

Считается сумма произведений цифр исходной системы счисления (предварительно переведённых в десятичную систему счисления) на веса разрядов (основание системы счисления в степени номер разряда, начиная с нулевого) в исходной системе. Полученное число является записью исходного числа в десятичной системе счисления.

Пример перевода 2→10

Ссылки

• Участник:Logic-samara