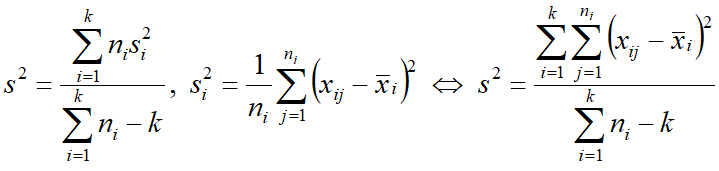Гипотеза о равенстве нескольких дисперсий
Гипотеза о равенстве нескольких дисперсий — гипотеза о том, что дисперсии k-совокупностей равны.
Обозначения
<math>k</math> — число совокупностей или выборок <math>X_i</math>, <math>k > 2</math>;
<math>n_i</math> — число значений в выборке <math>X_i</math>;
<math>D_{i \text{Г}}</math> — дисперсия генеральной совокупности <math>X_i</math>;
<math>\bar x_i</math> — средняя в выборке <math> X_i</math>, <math> \bar x_i = \frac{1}{n_i} \sum\limits_{j=1}^{n_i}{x_{ij}}</math>;
<math>D_{i \text{В}} = {s_i}^2</math> — дисперсия выборки <math>X_i</math>;
<math>s_i</math> — среднеквадратическое отклонение в выборке <math>X_i</math>, <math>s_i = \sqrt{\frac{1}{n_i}\sum\limits_{j=1}^{n_i}(x_{ij}- \bar x_i)^2}</math>;
α — уровень значимости — вероятность ошибки 1-го рода;
X2 — переменная X2-распределения.
FX2(X2,k-1) — интегральная функция X2-распределения.
Гипотезы о дисперсиях
 — критерий Бартлетта — статистика, имеющая X2-распределение, где
— критерий Бартлетта — статистика, имеющая X2-распределение, где
Пример 1
- <math>H_0: D_{1 \text{Г}} = D_{2 \text{Г}} = \ldots = D_{k \text{Г}};</math>
- <math>H_1:</math> альтернативная <math> H_0 </math> гипотеза;
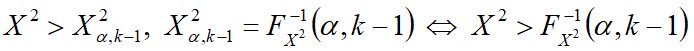 — критерий отклонения гипотезы H0.
— критерий отклонения гипотезы H0.
Другие гипотезы:
- Гипотеза о средней равной числу при известной дисперсии;
- Гипотеза о средней равной числу при неизвестной дисперсии;
- Гипотеза о дисперсии равной числу при известной средней;
- Гипотеза о дисперсии равной числу при неизвестной средней;
- Гипотеза о равенстве дисперсий;
- Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий;
- Гипотеза о равенстве нескольких дисперсий;
- Гипотеза о равенстве средних при известных дисперсиях;
- Гипотеза о равенстве разности средних числу при известных дисперсиях;
- Гипотеза о равенстве средних при неизвестных равных дисперсиях;
- Гипотеза о равенстве средних при неизвестных дисперсиях;
- Гипотеза о вероятности равной числу;
- Гипотеза о равенстве вероятностей;
- Гипотеза о нормальном законе распределения;
- Гипотеза об отсутствии линейной корреляционной связи;
- Гипотеза о коэффициенте линейного уравнения регрессии равном нулю;
- Гипотеза о коэффициенте линейного уравнения множественной регрессии равном нулю;
- Гипотеза о значимости линейного уравнения регрессии;
- Гипотеза о значимости линейного уравнения множественной регрессии;
- Гипотеза о коэффициенте корреляции равном числу;
- Гипотеза о коэффициенте корреляции равном нулю;
- Гипотеза о равенстве коэффициентов корреляции.