Гипотеза о нормальном законе распределения

Гипотеза о нормальном законе распределения — это гипотеза о соответствии распределения случайной величины нормальному распределению, N(μ,σ²).

Обозначения

n — число значений в интервальном ряду;

m — число интервалов;

x_j-1 — нижняя граница j-ого интервала, 1≤j≤m;

x_j — верхняя граница j-ого интервала, 1≤j≤m;

m_j — эмпирическая частота значений случайной величины в j-ом интервале;

μ — средняя нормального распределения;

σ — среднеквадратическое отклонение нормального распределения;

D=σ² — дисперсия нормального распределения;

p_j — теоретическая вероятность значений случайной величины в j-ом интервале;

u — переменная стандартизованной случайной величины;

Φ(u) — интегральная функция распределения стандартизованной случайной величины;

α — уровень значимости — вероятность ошибки 1-го рода;

X² — переменная X²-распределения.

k — число степеней свободы, k=m-3;

F_X²(X²,k) — интегральная функция X²-распределения.

Гипотеза о распределении:

— статистика, имеющая X²-распределение c (k=m-3) степенями свободы, где .

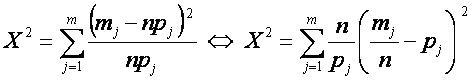
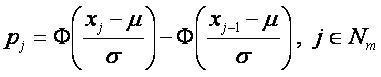
Для проверки гипотезы о нормальном распределении эмпирического распределения, строится интервальный ряд и определяются интервальные частоты (m_j) и теоретические вероятности (p_j).

H₀: закон нормального распределения N(μ,σ²);

H₁: другой закон распределения;

Критерий 1

— критерий отклонения гипотезы H₀.

Критерий 2

— критерий принятия гипотезы H₀.

Правило ван дер Вардена

Если для всех m интервалов, фактических частот (m_j), теоретические вероятности p_j больше табличного p_min (соответствующего числу степеней свободы k=m-3), то гипотеза H₀ проверяется при этих данных.

Если есть крайние интервалы для которых теоретические вероятности p_j меньше допустимого табличного p_min, то такие крайние интервалы объединяются с соседними (соответствующими интервалами) и гипотеза H₀ проверяется для изменённого m, для изменённых фактических частот (m_j), для изменённых теоретических вероятностей (p_j) и для изменённого числа степеней свободы (k=m-3).

Таблица допустимых теоретических вероятностей

Другие гипотезы:

1. Гипотеза о средней равной числу при известной дисперсии;
2. Гипотеза о средней равной числу при неизвестной дисперсии;
3. Гипотеза о дисперсии равной числу при известной средней;
4. Гипотеза о дисперсии равной числу при неизвестной средней;
5. Гипотеза о равенстве дисперсий;
6. Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий;
7. Гипотеза о равенстве нескольких дисперсий;
8. Гипотеза о равенстве средних при известной дисперсии;
9. Гипотеза о равенстве средних при неизвестной дисперсии;
10. Гипотеза о равенстве средних при неизвестных дисперсиях;
11. Гипотеза о вероятности равной числу;
12. Гипотеза о равенстве вероятностей;
13. Гипотеза о нормальном законе распределения;
14. Гипотеза об отсутствии линейной корреляционной связи;
15. Гипотеза о коэффициенте линейного уравнения регрессии равном нулю;
16. Гипотеза о коэффициенте линейного уравнения множественной регрессии равном нулю;
17. Гипотеза о значимости линейного уравнения регрессии;
18. Гипотеза о значимости линейного уравнения множественной регрессии;
19. Гипотеза о коэффициенте корреляции равном числу;
20. Гипотеза о коэффициенте корреляции равном нулю;
21. Гипотеза о равенстве коэффициентов корреляции.

Ссылки

• Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2004, стр.375.
• Участник:Logic-samara