Гипотеза о значимости линейного уравнения множественной регрессии

Гипотеза о значимости линейного уравнения множественной регрессии — гипотеза о равенстве нулю всех коэффициентов регрессии при независимых переменных.

Обозначения

n — число значений в выборке;

k — число независимых переменных;

<math>y = b_0 + b_1x_1 + b_2x_2 + \ldots + b_kx_k</math> — линейное уравнение множественной регрессии;

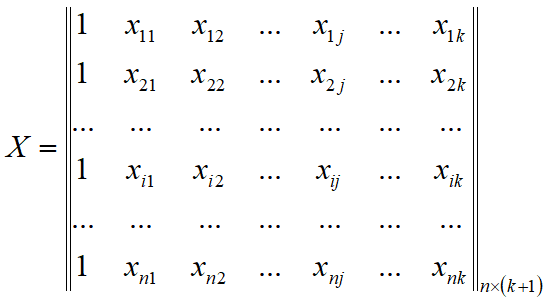— матрица значений независимых переменных в выборке;

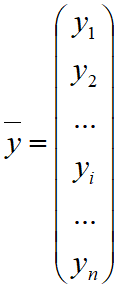— значения зависимой переменной; 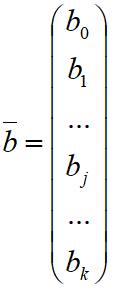— коэффициенты уравнения регрессии;

n-k-1 — число степеней свободы;

N_k — множество натуральных чисел j, 1≤j≤k.

F_F(F,k1,k2) — интегральная функция распределения Фишера-Снедекора.

F_табл(α_табл,k,n-k-1)=F_F^-1(1-α_табл,k,n-k-1) — табличное значение для F.

Гипотеза о значимости уравнения множественной регрессии

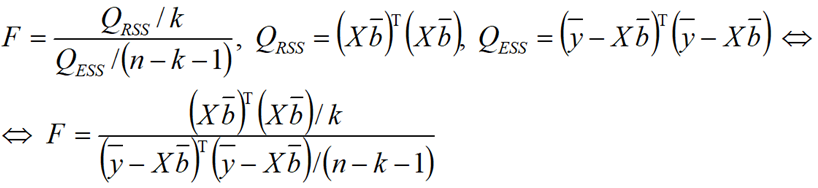Файл:СТФ21.png — статистика, имеющая распределение Фишера-Снедекора

Пример 1

<math>H_0: \text{Ɐ j ϵ } N_k , b_j=0;</math>

<math>H_1: \text{ⱻ j ϵ } N_k , \text{т.ч. } b_j \text{≠} 0;</math>

Файл:СТФ22.png — критерий отклонения гипотезы H₀.

Другие гипотезы

1. Гипотеза о средней равной числу при известной дисперсии;
2. Гипотеза о средней равной числу при неизвестной дисперсии;
3. Гипотеза о дисперсии равной числу при известной средней;
4. Гипотеза о дисперсии равной числу при неизвестной средней;
5. Гипотеза о равенстве дисперсий;
6. Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий;
7. Гипотеза о равенстве нескольких дисперсий;
8. Гипотеза о равенстве средних при известной дисперсии;
9. Гипотеза о равенстве средних при неизвестной дисперсии;
10. Гипотеза о равенстве средних при неизвестных дисперсиях;
11. Гипотеза о вероятности равной числу;
12. Гипотеза о равенстве вероятностей;
13. Гипотеза о нормальном законе распределения;
14. Гипотеза об отсутствии линейной корреляционной связи;
15. Гипотеза о коэффициенте линейного уравнения регрессии равном нулю;
16. Гипотеза о коэффициенте линейного уравнения множественной регрессии равном нулю;
17. Гипотеза о значимости линейного уравнения регрессии;
18. Гипотеза о значимости линейного уравнения множественной регрессии;
19. Гипотеза о коэффициенте корреляции равном числу;
20. Гипотеза о коэффициенте корреляции равном нулю;
21. Гипотеза о равенстве коэффициентов корреляции.

Ссылки

• Участник:Logic-samara