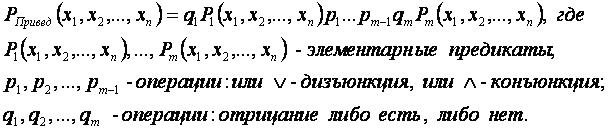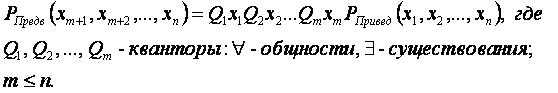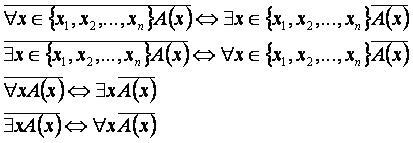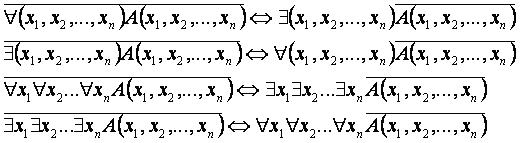Предикат

Предикаты — это предложения, высказывания, соотношения, выражения, функции, относительно которых при заданных аргументах, можно сказать, истинны они или ложны, т.е. они принимают значения из множества {0,1}.

Предикаты обозначаются прописными буквами с перечнем аргументов в скобках (как у функции). Набор аргументов определяется на произвольных множествах. Аргументы обозначаются строчными буквами

Содержание

1 Виды предикатов:
2 Виды операций:
- 2.1 Логические операции:
- 2.2 Кванторные операции:
3 Формы предикатов:
- 3.1 Приведённая нормальная форма
- 3.2 Предварённая нормальная форма
4 Свойства предикатов
5 Другие понятия:
6 Ссылки

Виды предикатов:

тождественно-истинный;
тождественно-ложный;
выполнимый.

Предикат называют тождественно-истинным (тавтологией), если на любом наборе аргументов он принимает значение 1.

Предикат называют тождественно-ложным (противоречием), если на любом наборе аргументов он принимает значение 0.

Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1.

Так как предикаты принимают только два значения, то к ним применимы все логические операции булевой алгебры.

Логическая функция является предикатом.
Логический закон является тождественно истинным предикатом.

Виды операций:

логические операции;
кванторные операции.

Логические операции:

отрицание;
дизъюнкция;
конъюнкция;
импликация.

Отрицанием предиката A(x) называется новый предикат C(x), который принимает значение истина при всех значениях x из заданного множества, при которых предикат A(x) принимает значение ложь, и принимает значение ложь, если A(x) принимает значение истина.

Дизъюнкцией двух предикатов A(x) и B(x) называется новый предикат C(x), который принимает значение ложь при тех и только тех значениях x из заданного множества, при которых каждый из предикатов принимает значение ложь и принимает значение истина во всех остальных случаях. Областью истинности предиката C(x) является объединение областей истинности предикатов A(x) и B(x).

Конъюнкцией двух предикатов A(x) и B(x) называется новый предикат C(x), который принимает значение истина при тех и только тех значениях х из заданного множества, при которых каждый из предикатов принимает значение истина, и принимает значение ложь во всех остальных случаях. Областью истинности предиката C(x) является пересечение областей истинности предикатов A(x) и B(x).

Импликацией предикатов A(x) и B(x) называется новый предикат C(x), который является ложным при тех и только тех значениях х из заданного множества, при которых A(x) принимает значение истина, а B(x) — значение ложь, и принимает значение истина во всех остальных случаях.

Кванторные операции:

квантор общности;
квантор существования.

Квантором общности называется операция, по которой предикату A(x) ставится в соответствие высказывание, обозначаемое , которое истинно тогда и только тогда, когда предикат A(x) тождественно истинен.

Высказывание читается: «Для любого х справедливо A(x)».

Квантором существования называется операция, по которой предикату A(x) ставится в соответствие высказывание, обозначаемое , которое ложно тогда и только тогда, когда предикат A(x) тождественно ложен.

Высказывание читается: «Существует такое х (хотя бы одно), что справедливо A(x)».

Формы предикатов:

приведённая нормальная форма;
предварённая нормальная форма.

Приведённая нормальная форма

Предварённая нормальная форма

Свойства предикатов

Если предикат A(x) определён на множестве, состоящем из конечного числа элементов x₁, x₂, …, x_n, то квантор общности можно трактовать как конъюнкцию всех возможных из него высказываний, а квантор существования – как дизъюнкцию этих высказываний.