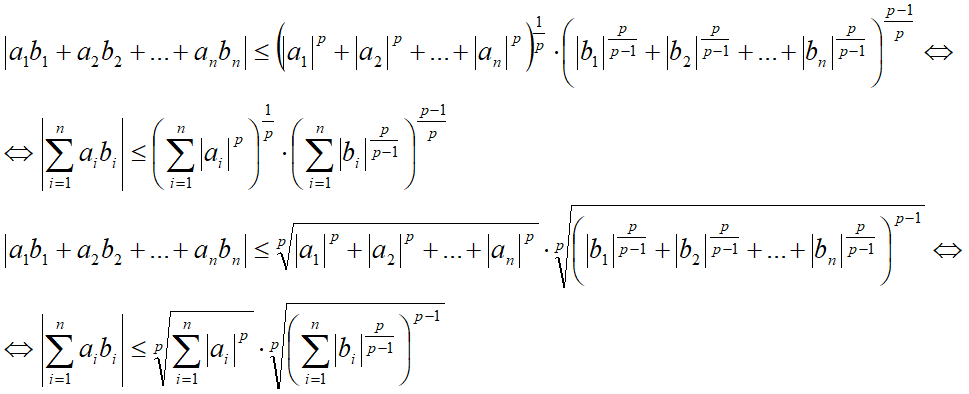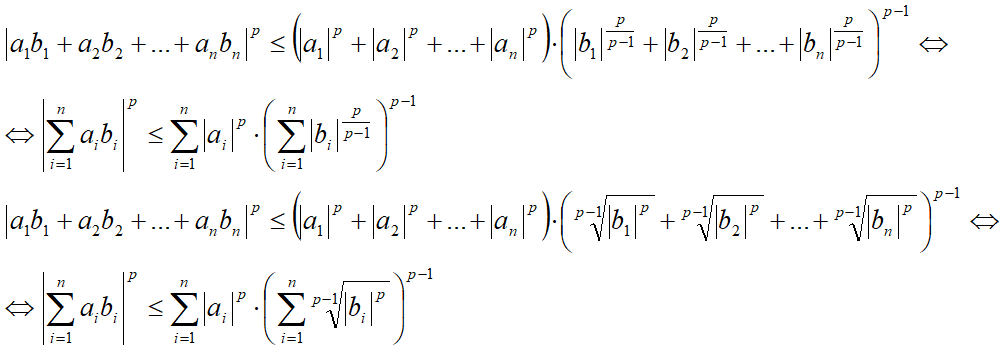Неравенство Гёльдера — различия между версиями
м |
м |
||
| (не показаны 4 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Модуль суммы произведений пар из двух наборов чисел не больше произведения 1/p-степени суммы p-степеней модулей первых элементов пар и (p-1)/p-степени суммы p/(1-p)-степеней модулей вторых элементов пар.''' | '''Модуль суммы произведений пар из двух наборов чисел не больше произведения 1/p-степени суммы p-степеней модулей первых элементов пар и (p-1)/p-степени суммы p/(1-p)-степеней модулей вторых элементов пар.''' | ||
| − | == | + | == Обозначения == |
| − | |||
| − | |||
'''n''' – число чисел в наборах; | '''n''' – число чисел в наборах; | ||
| Строка 10: | Строка 8: | ||
'''b<sub>i</sub>''' – '''i'''-ое число. | '''b<sub>i</sub>''' – '''i'''-ое число. | ||
| − | + | == Формула неравенства == | |
| − | [[файл:НГ01. | + | [[файл:НГ01.png]] |
*Заметим, что при '''p=2''' получаем [[неравенство Коши-Буняковского]]. | *Заметим, что при '''p=2''' получаем [[неравенство Коши-Буняковского]]. | ||
== Следствие == | == Следствие == | ||
| − | [[файл:НГ02. | + | [[файл:НГ02.png]] |
== [[Неравенства|Другие неравенства:]] == | == [[Неравенства|Другие неравенства:]] == | ||
{{Список Нер}} | {{Список Нер}} | ||
Текущая версия на 12:17, 14 февраля 2025
Модуль суммы произведений пар из двух наборов чисел не больше произведения 1/p-степени суммы p-степеней модулей первых элементов пар и (p-1)/p-степени суммы p/(1-p)-степеней модулей вторых элементов пар.
Обозначения
n – число чисел в наборах;
p – число больше 1;
ai – i-ое число;
bi – i-ое число.
Формула неравенства
- Заметим, что при p=2 получаем неравенство Коши-Буняковского.
Следствие
Другие неравенства:
- неравенство n-степени числа;
- неравенство Йенсена;
- неравенство Коши;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
