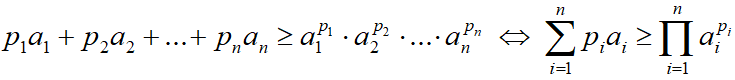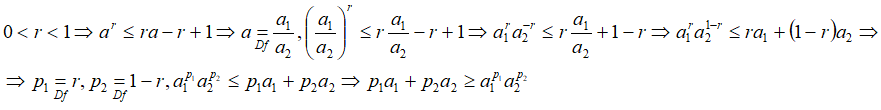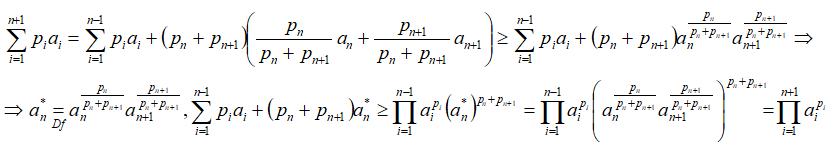Неравенство средних взвешенных

Неравенство средних взвешенных

Неравенство средних взвешенных – средневзвешенная сумма не меньше средневзвешенного произведения.

Обозначения

n – число положительных чисел;

a_i – i-ое положительное число;

p_i – i-ый удельный вес, 0<p_i<1;

p₁+p₂+...+p_n=1 – сумма весов.

Формула неравенства

• При p_i=1/n для всех i получаем неравенство Коши.

Доказательство

1.Докажем неравенство при k=2.

т.е. неравенство верно при k=2.

2.Доказательство индукцией вверх. Предполагаем, что неравенство верно для k=n-1, и доказываем неравенство для k=n.

т.е. неравенство верно при k=n, ч.т.д.

• При доказательстве используется неравенство r-степени числа.

Другие неравенства:

• неравенство n-степени числа;
• неравенство r-степени числа;
• неравенство Йенсена;
• неравенство Коши;
• неравенство средних взвешенных;
• неравенство p-ичных средних;
• обобщённое неравенство средних;
• неравенство взвешенных p-ичных средних;
• неравенство Коши-Буняковского;
• интегральное неравенство Коши-Буняковского;
• неравенство Минковского;
• обобщённое неравенство Минковского;
• интегральное неравенство Минковского;
• неравенство Гёльдера;
• обобщённое неравенство Гёльдера;
• интегральное неравенство Гёльдера;
• неравенство Фань Цзы;
• неравенство Маркова;
• неравенство Чебышёва.

Литература

• Беккенбах Э., Беллман Р. Неравенства. М.: КомКнига, под ред. В.И.Левина, Изд.2, 2007, стр.26.