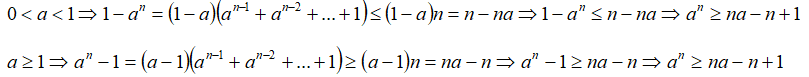Неравенство n-степени числа — различия между версиями
(начало) |
м |
||
| (не показано 7 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | + | [[Файл:НСЧ01.png|thumb|300px|Неравенство n-степени числа]] | |
| + | '''Неравенство ''n''-степени числа – положительное число ''a'' в степени ''n'' не меньше выражения ''na-n+1''.''' | ||
== Обозначения == | == Обозначения == | ||
'''n''' – натуральное число; | '''n''' – натуральное число; | ||
| Строка 10: | Строка 11: | ||
== [[Неравенства|Другие неравенства:]] == | == [[Неравенства|Другие неравенства:]] == | ||
{{Список Нер}} | {{Список Нер}} | ||
| − | == | + | == Литература == |
| − | *Беккенбах Э., Беллман Р. Неравенства. М.: КомКнига, под ред. В.И.Левина, Изд.2, 2007, стр.23. [[Категория:Математика]] | + | *Беккенбах Э., Беллман Р. Неравенства. М.: КомКнига, под ред. В.И.Левина, Изд.2, 2007, стр.23. |
| + | [[Категория:Математика]] | ||
Текущая версия на 10:20, 24 марта 2025
Неравенство n-степени числа – положительное число a в степени n не меньше выражения na-n+1.
Обозначения
n – натуральное число;
a – положительное число.
Формула неравенства
Доказательство
Другие неравенства:
- неравенство n-степени числа;
- неравенство Йенсена;
- неравенство Коши;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
Литература
- Беккенбах Э., Беллман Р. Неравенства. М.: КомКнига, под ред. В.И.Левина, Изд.2, 2007, стр.23.
