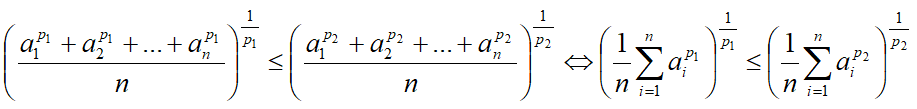Неравенство p-ичных средних — различия между версиями
м |
м |
||
| Строка 1: | Строка 1: | ||
[[Файл:НС01.png|thumb|300px|Неравенство p-ичных средних]] | [[Файл:НС01.png|thumb|300px|Неравенство p-ичных средних]] | ||
| − | '''Неравенство ''p''-ичных средних – | + | '''Неравенство ''p''-ичных средних – для отличных от нуля действительных ''p'' из двух ''p''-ичных средних положительных чисел, средняя для меньшего ''p'' не больше средней для большего ''p''.''' |
== Обозначения == | == Обозначения == | ||
'''n''' – число положительных чисел; | '''n''' – число положительных чисел; | ||
Текущая версия на 10:24, 24 марта 2025
Неравенство p-ичных средних – для отличных от нуля действительных p из двух p-ичных средних положительных чисел, средняя для меньшего p не больше средней для большего p.
Обозначения
n – число положительных чисел;
p1 – меньшая степень p-ичной средней;
p2 – большая степень p-ичной средней;
ai – i-ое положительное число.
Формула неравенства
Следствие
- В двойных неравенствах следствия, левое неравенство получается из формулы при p1=-1 и p2=1, а правое – при p1=1 и p2=2.
- Двойное неравенство следствия означает, что: xср.гарм.≤xср.арифм.≤xср.квадр.
Другие неравенства:
- неравенство n-степени числа;
- неравенство Йенсена;
- неравенство Коши;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
