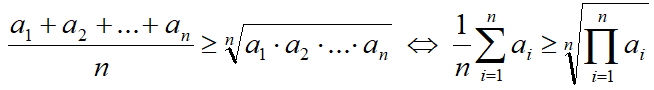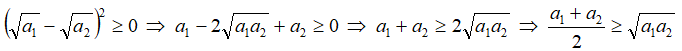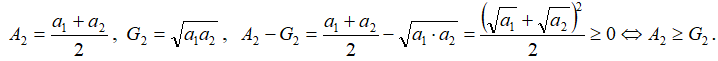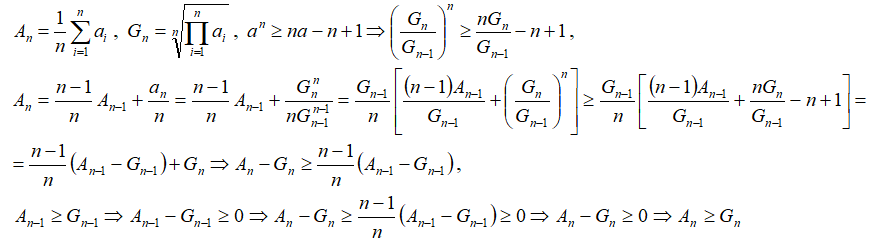Неравенство Коши — различия между версиями
м |
м |
||
| Строка 1: | Строка 1: | ||
'''Среднее арифметическое n''' положительных чисел не меньше их '''среднего геометрического'''. | '''Среднее арифметическое n''' положительных чисел не меньше их '''среднего геометрического'''. | ||
| − | == | + | == Обозначения == |
'''n''' – число чисел; | '''n''' – число чисел; | ||
'''a<sub>i</sub>''' – '''i'''-ое положительное число; | '''a<sub>i</sub>''' – '''i'''-ое положительное число; | ||
| − | [[файл:НК01. | + | '''b<sub>i</sub>''' – это число равное '''lna<sub>i</sub>'''. |
| − | == | + | == Формула неравенства == |
| − | [[ | + | [[файл:НК01.png]] |
| + | *Равенство имеет место только в том случае, когда все '''a <sub>i</sub>''' равны между собой. | ||
| + | |||
| + | == Доказательство == | ||
| + | 1.Докажем неравенство при '''k=2'''. | ||
| + | |||
| + | [[Файл:НК11.png]] | ||
| + | |||
| + | т.е. неравенство верно при '''k=2'''. | ||
| + | |||
| + | 2.Доказательство [[Метод математической индукции|индукцией]] вверх. | ||
| + | Предполагаем, что неравенство верно для '''k=n''', и доказываем неравенство для '''k=2n'''. | ||
| + | [[Файл:НК12.png]] | ||
| − | + | т.е. неравенство верно при '''k=2n'''. | |
| − | [[ | + | 3.Доказательство [[Метод математической индукции|индукцией]] вниз. |
| + | Предполагаем, что неравенство верно для '''k=n''', и доказываем неравенство для '''k=n-1'''. | ||
| + | [[Файл:НК13.png]] | ||
| − | + | т.е. неравенство верно при '''k=n-1''', ч.т.д. | |
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
*Идея доказательства общеизвестна, мне о ней рассказал в 1973 году В. Г. Евстигнеев - преподаватель математики МИЭИ им. С. Орджоникидзе. | *Идея доказательства общеизвестна, мне о ней рассказал в 1973 году В. Г. Евстигнеев - преподаватель математики МИЭИ им. С. Орджоникидзе. | ||
| + | == Следствия == | ||
| + | [[файл:НК20.png]] | ||
| + | |||
| + | [[файл:НК21.png]] | ||
| + | |||
| + | [[файл:НК22.png]] | ||
== [[Неравенства|Другие неравенства:]] == | == [[Неравенства|Другие неравенства:]] == | ||
{{Список Нер}} | {{Список Нер}} | ||
Версия 05:28, 7 февраля 2025
Среднее арифметическое n положительных чисел не меньше их среднего геометрического.
Содержание
Обозначения
n – число чисел;
ai – i-ое положительное число;
bi – это число равное lnai.
Формула неравенства
- Равенство имеет место только в том случае, когда все a i равны между собой.
Доказательство
1.Докажем неравенство при k=2.
т.е. неравенство верно при k=2.
2.Доказательство индукцией вверх.
Предполагаем, что неравенство верно для k=n, и доказываем неравенство для k=2n.
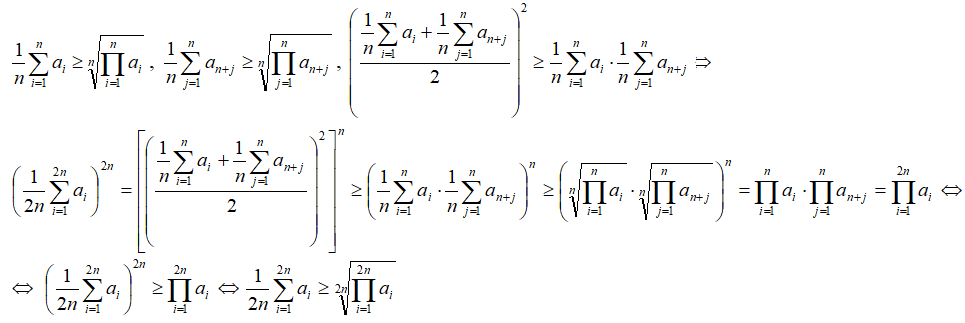
т.е. неравенство верно при k=2n.
3.Доказательство индукцией вниз.
Предполагаем, что неравенство верно для k=n, и доказываем неравенство для k=n-1.
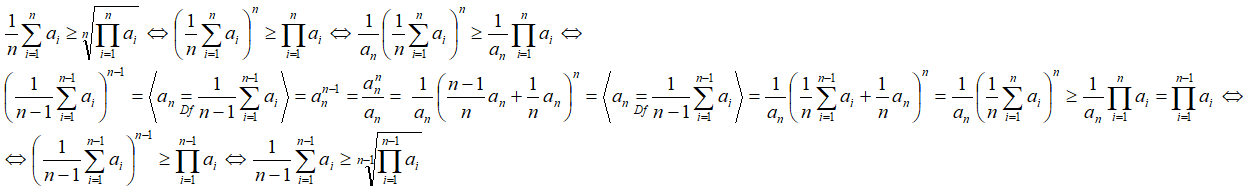
т.е. неравенство верно при k=n-1, ч.т.д.
- Идея доказательства общеизвестна, мне о ней рассказал в 1973 году В. Г. Евстигнеев - преподаватель математики МИЭИ им. С. Орджоникидзе.
Следствия
Другие неравенства:
- неравенство n-степени числа;
- неравенство r-степени числа;
- неравенство Йенсена;
- неравенство Юнга;
- неравенство Коши;
- неравенство средних взвешенных;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
Ссылки
- Беллман Р. Введение в теорию матриц. М.: Наука, 1976, стр.158.