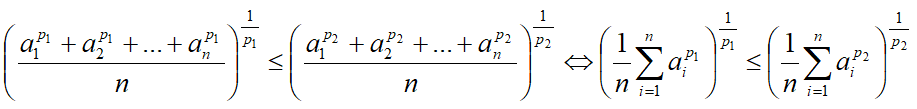Неравенство p-ичных средних — различия между версиями
м |
м |
||
| Строка 13: | Строка 13: | ||
[[файл:НC02.png]] | [[файл:НC02.png]] | ||
*В двойных неравенствах следствия, левое неравенство получается из формулы при '''p<sub>1</sub>=-1''' и '''p<sub>2</sub>=1''', а правое – при '''p<sub>1</sub>=1''' и '''p<sub>2</sub>=2'''. | *В двойных неравенствах следствия, левое неравенство получается из формулы при '''p<sub>1</sub>=-1''' и '''p<sub>2</sub>=1''', а правое – при '''p<sub>1</sub>=1''' и '''p<sub>2</sub>=2'''. | ||
| − | *Двойное неравенство следствия означает, что: '''x<sub>ср.гарм.</sub>≤x<sub>ср.арифм.</sub>≤x<sub>ср.квадр.</sub>''' | + | *Двойное неравенство следствия означает, что: '''x<sub>ср.гарм.</sub>≤x<sub>ср.арифм.</sub>≤x<sub>ср.квадр.</sub>''' |
== [[Неравенства|Другие неравенства:]] == | == [[Неравенства|Другие неравенства:]] == | ||
{{Список Нер}} | {{Список Нер}} | ||
Версия 09:32, 15 февраля 2025
Для отличных от нуля действительных p из двух p-ичных средних положительных чисел, средняя для меньшего p не больше средней для большего p.
Обозначения
n – число положительных чисел;
p1 – меньшая степень p-ичной средней;
p2 – большая степень p-ичной средней;
ai – i-ое положительное число.
Формула неравенства
Следствие
- В двойных неравенствах следствия, левое неравенство получается из формулы при p1=-1 и p2=1, а правое – при p1=1 и p2=2.
- Двойное неравенство следствия означает, что: xср.гарм.≤xср.арифм.≤xср.квадр.
Другие неравенства:
- неравенство n-степени числа;
- неравенство Йенсена;
- неравенство Коши;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
