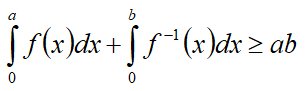Неравенство Юнга

Неравенство Юнга для строго возрастающей f(x)

Неравенство Юнга – для непрерывной строго возрастающей от нуля функции сумма интегралов от взаимно обратных функций от нуля до пределов интегрирования не меньше произведения этих пределов интегрирования.

Геометрический смысл: сумма площадей под графиком строго возрастающей функции и под графиком обратной функции не меньше площади прямоугольника со сторонами равными пределам интегрирования.

Обозначения

a, b – пределы интегрирования;

f(x) – строго возрастающая от нуля функция, 0≤x≤a, f(0)=0;

f^-1(x) – функция обратная к f(x), 0≤x≤b.

Формула неравенства

Другие неравенства:

• неравенство n-степени числа;
• неравенство r-степени числа;
• неравенство Йенсена;
• неравенство Юнга;
• неравенство Коши;
• неравенство средних взвешенных;
• неравенство p-ичных средних;
• обобщённое неравенство средних;
• неравенство взвешенных p-ичных средних;
• неравенство Коши-Буняковского;
• интегральное неравенство Коши-Буняковского;
• неравенство Минковского;
• обобщённое неравенство Минковского;
• интегральное неравенство Минковского;
• неравенство Гёльдера;
• обобщённое неравенство Гёльдера;
• интегральное неравенство Гёльдера;
• неравенство Фань Цзы;
• неравенство Маркова;
• неравенство Чебышёва.

Литература

• Беккенбах Э., Беллман Р. Неравенства. М.: КомКнига, под ред. В.И.Левина, Изд.2, 2007, стр.27.