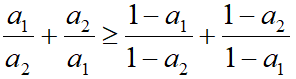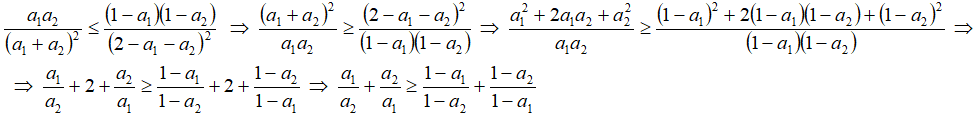Неравенство Фань Цзы

Файл:НФЦ01.PNG

300px

Неравенство Фань Цзы — неравенство для действительных чисел, гласящее, что отношение произведения n положительных дробей, не превышающих 0,5, к n-степени их суммы не больше аналогичного отношения для дополнений этих дробей до единицы.

Обозначения

n — число дробей;

<math>a_i</math> — i-ая положительная дробь от 0 до 0,5;

<math>1-a_i</math> — это дополнение <math>a_i</math> до 1 — положительная дробь от 0,5 до 1.

Формула неравенства

<math> \frac{a_1\cdot a_2\cdot \ldots \cdot a_n}{ \left(a_1+a_2+\ldots+a_n\right)^n } \le \frac{\left(1-a_1\right)\cdot \left(1-a_2\right)\cdot \ldots \cdot \left(1-a_n\right)}{\left[ \left(1-a_1\right)+\left(1-a_2\right)+\ldots+\left(1-a_n\right) \right]^n} \Leftrightarrow \frac{ \prod \limits_{i=1}^n a_i}{\left( \sum \limits_{i=1}^n a_i\right)^n} \le \frac{ \prod \limits_{i=1}^n \left(1-a_i \right)}{ \left[ \sum\limits_{i=1}^n \left(1-a_i\right) \right]^n}

</math>

• Равенство имеет место только в том случае, когда все a _i равны между собой.

Доказательство

1.Докажем неравенство при k=2.

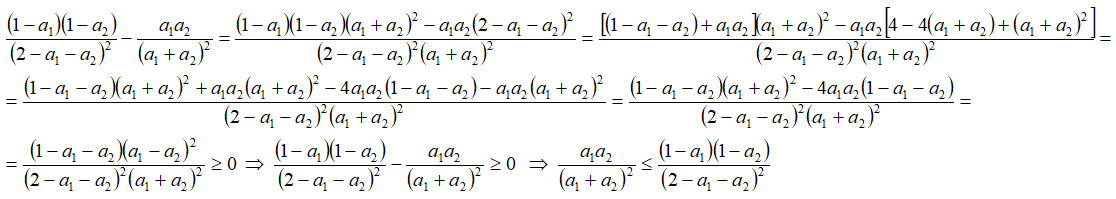
т.е. неравенство верно при k=2.

2.Доказательство индукцией вверх. Предполагаем, что неравенство верно для k=n, и доказываем неравенство для k=2n.

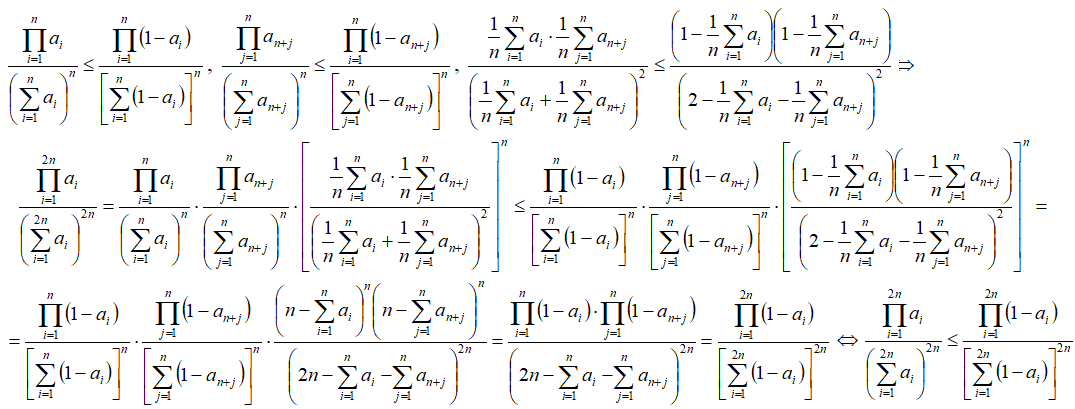
т.е. неравенство верно при k=2n.

3.Доказательство индукцией вниз. Предполагаем, что неравенство верно для k=n, и доказываем неравенство для k=n-1.

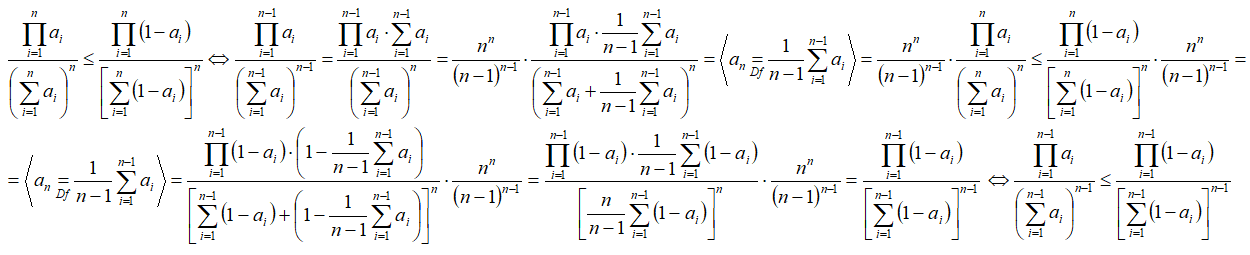
т.е. неравенство верно при k=n-1, ч.т.д.

Следствие

<math> \frac{a_1}{a_2}+\frac{a_2}{a_1} \ge \frac{1-a_1}{1-a_2}+ \frac{1-a_2}{1-a_1} </math>

Доказательство следствия

Другие неравенства:

• неравенство n-степени числа;
• неравенство Йенсена;
• неравенство Коши;
• неравенство p-ичных средних;
• обобщённое неравенство средних;
• неравенство взвешенных p-ичных средних;
• неравенство Коши-Буняковского;
• интегральное неравенство Коши-Буняковского;
• неравенство Минковского;
• обобщённое неравенство Минковского;
• интегральное неравенство Минковского;
• неравенство Гёльдера;
• обобщённое неравенство Гёльдера;
• интегральное неравенство Гёльдера;
• неравенство Фань Цзы;
• неравенство Маркова;
• неравенство Чебышёва.

Ссылки

• Беккенбах Э., Беллман Р. Неравенства. М.: КомКнига, под ред. В.И.Левина, Изд.2, 2007, стр.15.