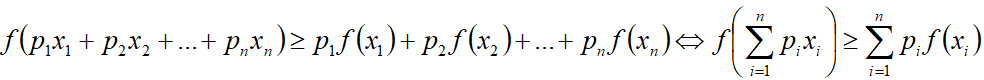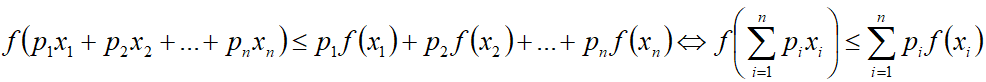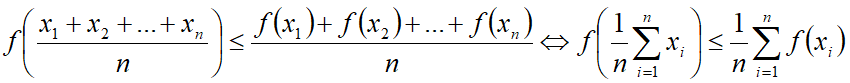Неравенство Йенсена

Неравенство Йенсена – выпуклая вверх функция от линейной комбинации чисел не менее линейной комбинации функций от этих чисел, выпуклая вниз функция от линейной комбинации чисел не более линейной комбинации функций от этих чисел.

Обозначения

n – число чисел;

x_i – i-ое число;

p_i – это i-ая положительная дробь, 0<p_i<1.

f(x) – функция;

p₁+p₂+…+p_n=1.

Формула неравенства

Функция выпукла вверх

Функция выпукла вниз

Следствия

Полагая, что p₁=p₂=…=p_n=1/n, получаем.

Функция выпукла вверх

Функция выпукла вниз

Другие неравенства:

• неравенство n-степени числа;
• неравенство Йенсена;
• неравенство Коши;
• неравенство p-ичных средних;
• обобщённое неравенство средних;
• неравенство взвешенных p-ичных средних;
• неравенство Коши-Буняковского;
• интегральное неравенство Коши-Буняковского;
• неравенство Минковского;
• обобщённое неравенство Минковского;
• интегральное неравенство Минковского;
• неравенство Гёльдера;
• обобщённое неравенство Гёльдера;
• интегральное неравенство Гёльдера;
• неравенство Фань Цзы;
• неравенство Маркова;
• неравенство Чебышёва.

Литература

• Зорич, В. А., Математический анализ. Ч.I, М, МЦНМО, 2012, с.289—290.
• Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, М, ФИЗМАТЛИТ, 2001, Т.1, с.336—337.

Ссылки

• https://ru.wikipedia.org/wiki/Неравенство_Йенсена