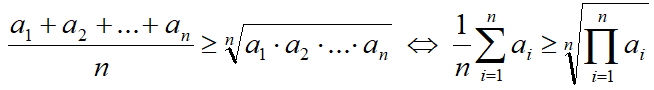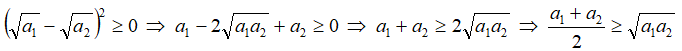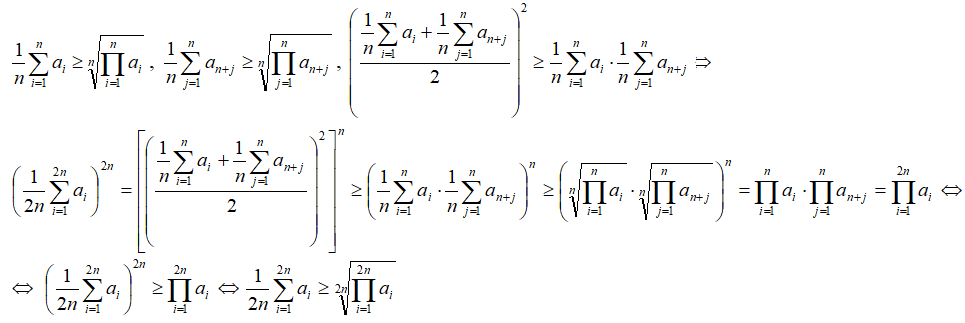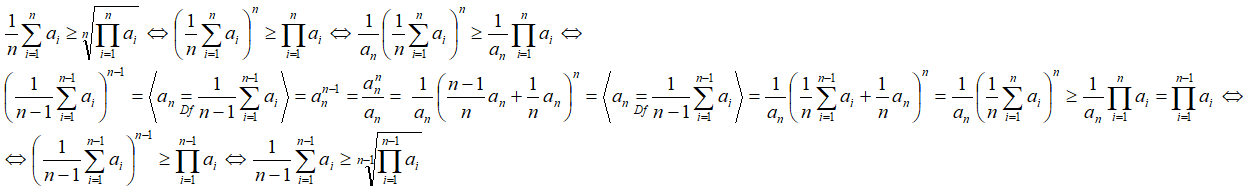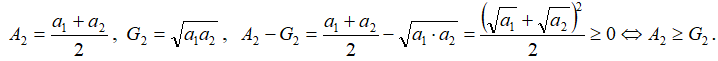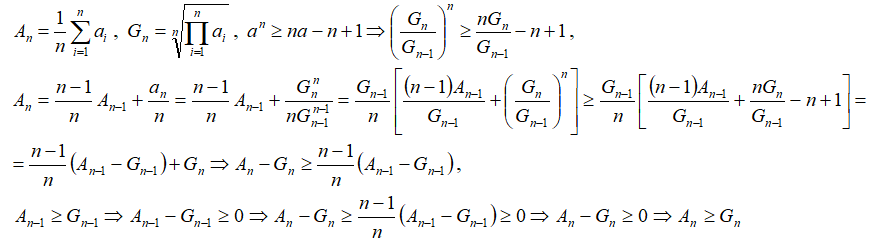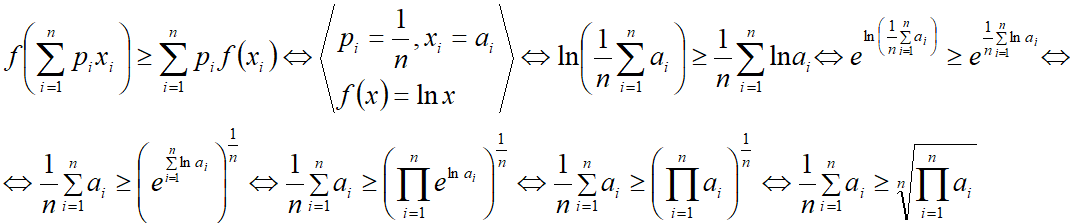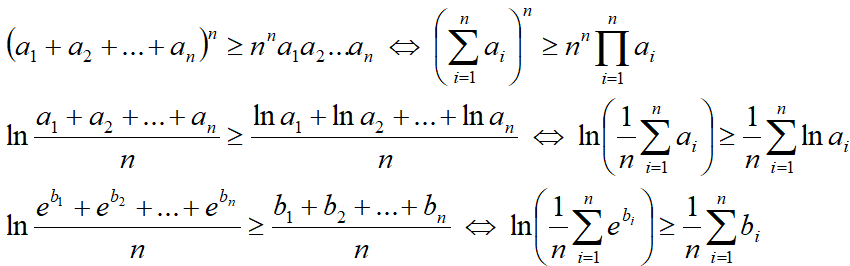Неравенство Коши
Неравенство Коши – среднее арифметическое n положительных чисел не меньше их среднего геометрического.
Содержание
Обозначения
n – число чисел;
ai – i-ое положительное число;
bi – это число равное ln ai.
Формула неравенства
- Равенство имеет место только в том случае, когда все ai равны между собой.
Доказательство 1
1.Докажем неравенство при k=2.
т.е. неравенство верно при k=2.
2.Доказательство индукцией вверх. Предполагаем, что неравенство верно для k=n и k=2, и доказываем неравенство для k=2n.
т.е. неравенство верно при k=2n.
3.Доказательство индукцией вниз. Предполагаем, что неравенство верно для k=n, и доказываем неравенство для k=n-1.
т.е. неравенство верно при k=n-1, ч.т.д.
- Идея доказательства общеизвестна, мне о ней рассказал в 1973 году В. Г. Евстигнеев - преподаватель математики МИЭИ им. С. Орджоникидзе.
Доказательство 2
1.Докажем неравенство при k=2.
т.е. неравенство верно при k=2.
2.Доказательство индукцией вверх. Предполагаем, что неравенство верно для k=n-1, и доказываем неравенство для k=n.
т.е. неравенство верно при k=n, ч.т.д.
- Автор идеи доказательства Э.Якобсталь, при доказательстве используется неравенство n-степени числа.
Доказательство 3
Т.к. функция lnx является функцией выпуклой вверх, то к ней применимо соответствующее неравенство Йенсена.
- Идея доказательства сформулирована в Википедии.
Следствия
Другие неравенства:
- неравенство n-степени числа;
- неравенство r-степени числа;
- неравенство Йенсена;
- неравенство Юнга;
- неравенство Коши;
- неравенство средних взвешенных;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
Ссылки
- Беллман Р. Введение в теорию матриц. М.: Наука, 1976, стр.158.
- Беккенбах Э., Беллман Р. Неравенства. М.: КомКнига, под ред. В.И.Левина, Изд.2, 2007, стр.24.