Гипотеза о равенстве вероятностей

Гипотеза о равенстве вероятностей — гипотеза о том, что вероятности двух совокупностей равны.

Для нормально распределённой случайной величины использует статистику, имеющую стандартизованное распределение, N(0;1).

Обозначения

n_x — число значений в выборке X;

n_y — число значений в выборке Y;

m_x — частота значений альтернативного признака в выборке X;

m_y — частота значений альтернативного признака в выборке Y;

w_x — относительная частота значений альтернативного признака в выборке X;

w_y — относительная частота значений альтернативного признака в выборке Y;

p_x — вероятность значений альтернативного признака в генеральной совокупности X;

p_y — вероятность значений альтернативного признака в генеральной совокупности Y;

α — уровень значимости — вероятность ошибки 1-го рода;

γ=1-α — коэффициент доверия;

x — переменная стандартизованной случайной величины;

u — статистика, распределённая по нормальному закону N(0;1);

Файл:ИФН02.png — интегральная функция нормального закона распределения стандартизованной случайной величины;

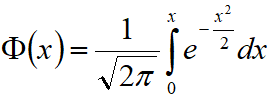— интегральная функция Лапласа, отличается от интегральной функции нормального закона для стандартизованной случайной величины на 0,5, т.е. Ф(x)=F(x)-0,5.

Гипотезы о вероятностях

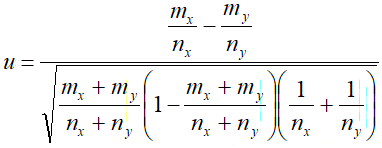Файл:СТН10.png — статистика, распределённая по нормальному закону N(0;1).

Пример 1

H₀:p_x=p_y;

H₁: p_x≠p_y;

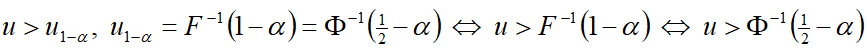Файл:СТН03.png — критерий отклонения гипотезы H₀.

Пример 2

H₀: p_x≤ p_y;

H₁: p_x> p_y;

Файл:СТН02.png — критерий отклонения гипотезы H₀.

• Заметим, что u_1-α=-u_α.

Пример 3

H₀: p_x≥p_y;

H₁: p_x< p_y;

Файл:СТН04.png — критерий отклонения гипотезы H₀.

• Заметим, что u_α=-u_1-α.

Пример 4

H₀:p_x≠p_y;

H₁:p_x= p_y;

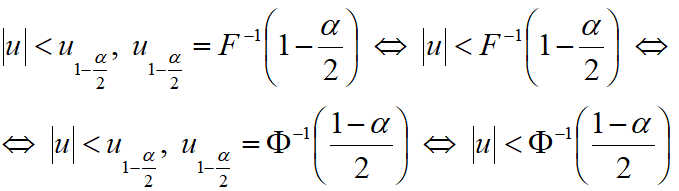Файл:СТН05.png — критерий отклонения гипотезы H₀.

Другие гипотезы

1. Гипотеза о средней равной числу при известной дисперсии;
2. Гипотеза о средней равной числу при неизвестной дисперсии;
3. Гипотеза о дисперсии равной числу при известной средней;
4. Гипотеза о дисперсии равной числу при неизвестной средней;
5. Гипотеза о равенстве дисперсий;
6. Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий;
7. Гипотеза о равенстве нескольких дисперсий;
8. Гипотеза о равенстве средних при известной дисперсии;
9. Гипотеза о равенстве средних при неизвестной дисперсии;
10. Гипотеза о равенстве средних при неизвестных дисперсиях;
11. Гипотеза о вероятности равной числу;
12. Гипотеза о равенстве вероятностей;
13. Гипотеза о нормальном законе распределения;
14. Гипотеза об отсутствии линейной корреляционной связи;
15. Гипотеза о коэффициенте линейного уравнения регрессии равном нулю;
16. Гипотеза о коэффициенте линейного уравнения множественной регрессии равном нулю;
17. Гипотеза о значимости линейного уравнения регрессии;
18. Гипотеза о значимости линейного уравнения множественной регрессии;
19. Гипотеза о коэффициенте корреляции равном числу;
20. Гипотеза о коэффициенте корреляции равном нулю;
21. Гипотеза о равенстве коэффициентов корреляции.

Ссылки

• Кремер Н.Ш., Путко И.М., Тришин И.М. Математика для экономистов: от Арифметики до Эконометрики. М.: Высшее образование, 2007, стр.353.
• Участник:Logic-samara