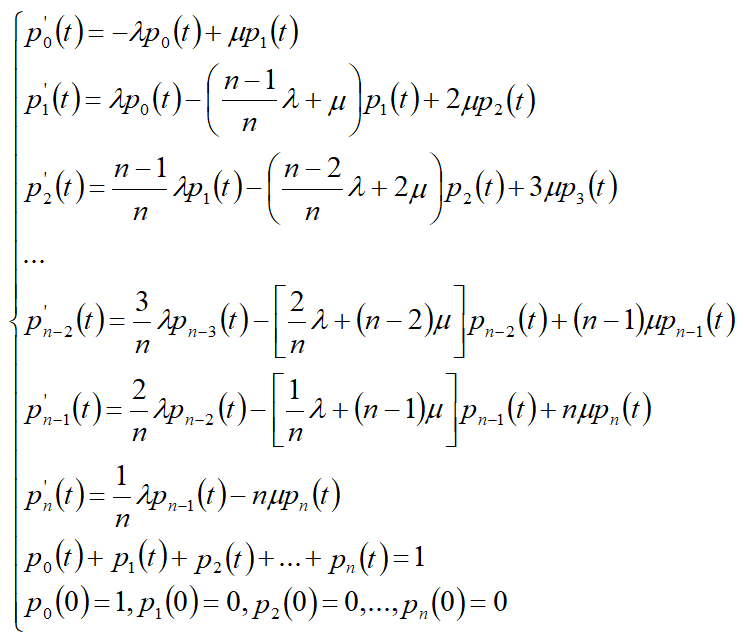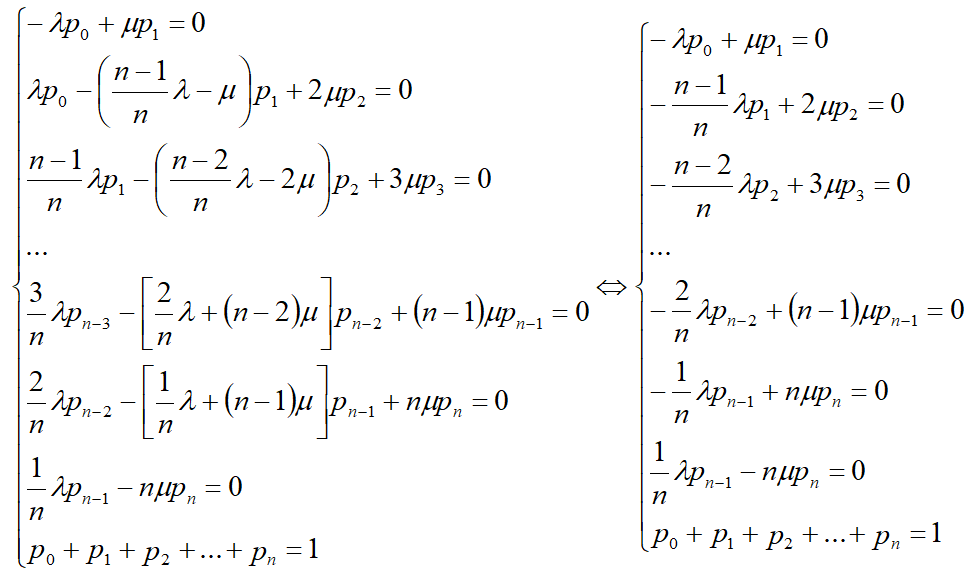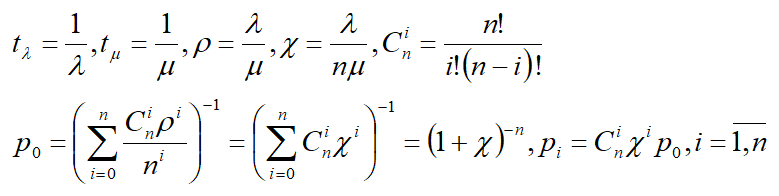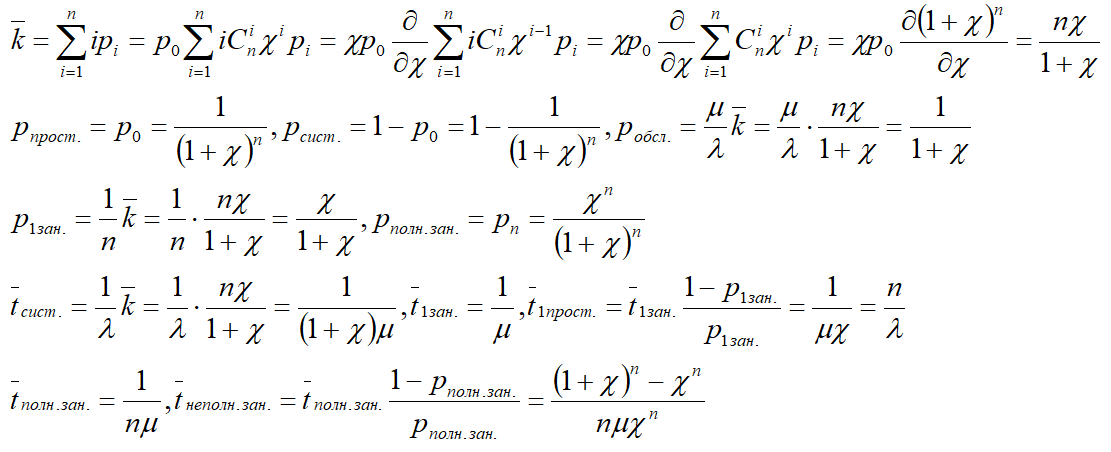СМО n-канальная без очереди и со случайным выбором канала

СМО n-канальная без очереди и со случайным выбором канала

СМО n-канальная без очереди и со случайным выбором канала — это система массового обслуживания, в которой есть каналы обслуживания, но нет очереди: если заявка приходит, в момент, когда все каналы свободны, то она немедленно обслуживается случайным одним каналом, если заявка приходит - когда уже обслуживаются заявки числом меньше, чем число каналов, то она случайно распределяется между всеми каналами, если выбранный канал свободен, то заявка обслуживается, иначе заявка покидает систему не обслуженной, если заявка приходит - когда заняты все каналы, то заявка покидает систему (теряется). Максимальное число заявок в системе равно числу каналов.

Описание модели

На вход n-канальной СМО поступает простейший поток заявок с интенсивностью λ.

Интенсивность простейшего потока обслуживания каждого канала μ.

Если заявка застаёт все каналы свободными, она принимается на обслуживание и обслуживается случайным одним из n-каналов.

Если заявка приходит, когда уже обслуживаются заявки числом меньше, чем число каналов, то она случайно распределяется между всеми каналами, если выбранный канал свободен, то заявка обслуживается, иначе заявка покидает систему не обслуженной.

Если заявка застаёт все каналы занятыми, то она получает отказ (покидает систему не обслуженной).

После окончания обслуживания одной заявки освобождается один канал.

Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе.

Граф состояний

М/М/n/0 – СМО n-канальная без очереди и со случайным выбором канала.

Рассмотрим множество состояний системы:

S₀ – в системе нет ни одной заявки, все каналы свободны;

S₁ – в системе имеется 1-заявка, она обслуживается 1-каналом;

S₂ – в системе имеется 2-заявки, они обслуживается 2-каналами;

…;

S_i-1 – в системе имеется (i-1)-заявок, они обслуживаются (i-1)-каналами;

S_i – в системе имеется i-заявок, они обслуживаются i-каналами.

S_i+1 – в системе имеется (i+1)-заявок, они обслуживаются (i+1)-каналами;

…;

S_n-2 – в системе имеется (n-2)-заявок, они обслуживаются (n-2)-каналами;

S_n-1 – в системе имеется (n-1)-заявок, они обслуживаются (n-1)-каналами;

S_n – в системе имеется n-заявок, они обслуживаются n-каналами.

Система дифференциальных уравнений

Рассмотрим стационарный режим работы системы (при t→∞).

Система линейных уравнений

Система уравнений принимает вид:

Суммируя в системе уравнения с первого до i-го (i=1,n), получаем упрощённый вид системы.

Решение системы линейных уравнений

Решим систему относительно p₀,p₁,p₂,…,p_n.

В результате получаем решение системы:

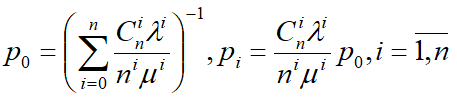
Основные характеристики системы

Другие СМО:

• СМО n-канальная без очереди;
• СМО n-канальная без очереди и со случайным выбором канала;
• СМО n-канальная с m-очередью;
• СМО n-канальная с m-очередью и с ограниченным временем ожидания;
• СМО с бесконечным числом каналов;
• СМО n-канальная с бесконечной очередью;
• СМО n-канальная без очереди и с взаимопомощью;
• СМО n-канальная с m-очередью и с взаимопомощью;
• СМО замкнутая n-канальная без очереди;
• СМО замкнутая n-канальная с m-очередью;
• СМО замкнутая n-канальная без очереди и с k-источниками;
• СМО замкнутая n-канальная с m-очередью и с k-источниками.

Ссылки

• Овчаров Л.А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969,стр.151-154.