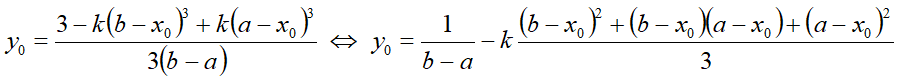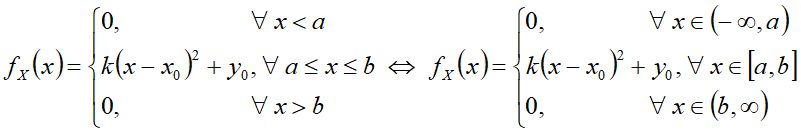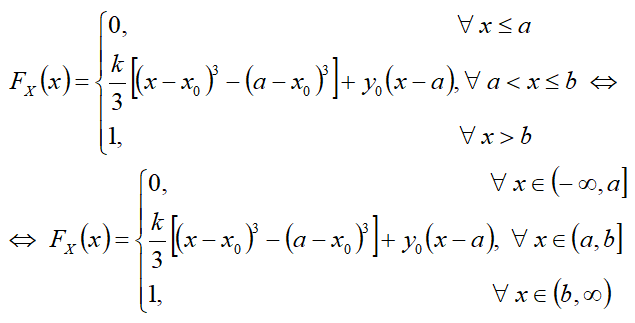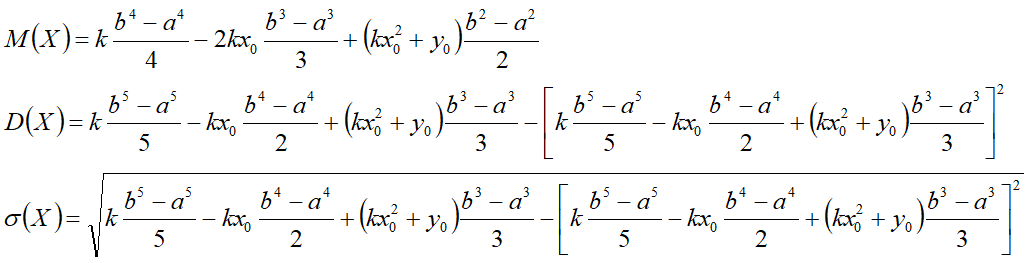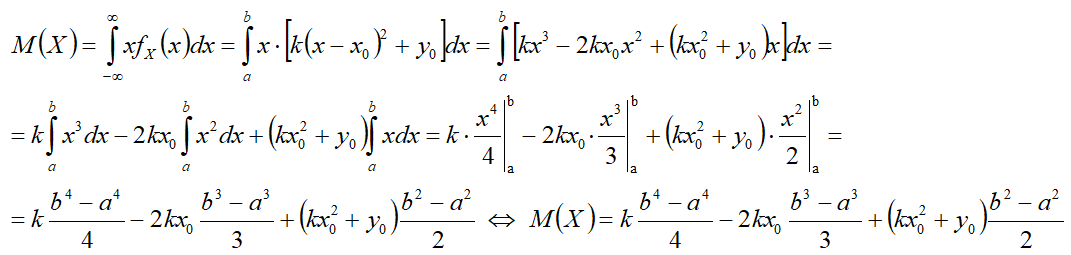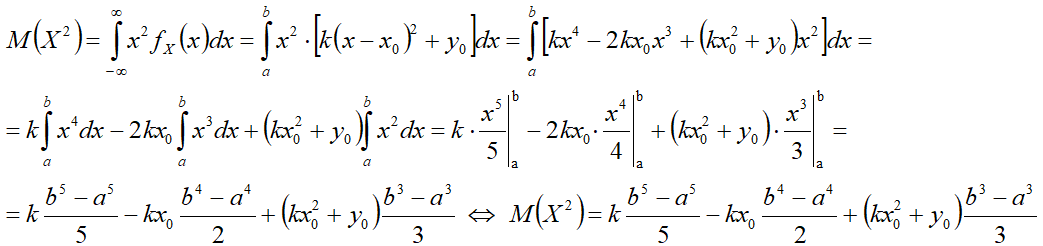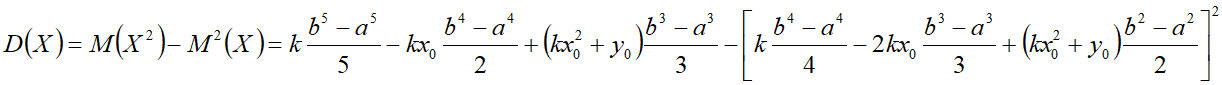Квадратичное распределение — различия между версиями

Материал из Мегапедии
Перейти к: навигация, поиск
 
(не показаны 2 промежуточные версии этого же участника)
Строка 11: Строка 11:
 
'''b''' — верхняя граница отрезка;
 
'''b''' — верхняя граница отрезка;
  
−
'''α''' — коэффициент параболы;
+
'''k''' — коэффициент параболы;
  
−
'''β''' — абсцисса вершины параболы параболы;
+
'''x<sub>0</sub>''' — абсцисса вершины параболы;
  
−
'''γ''' — ордината вершины параболы параболы;
+
'''y<sub>0</sub>''' — ордината вершины параболы;
  
 
'''M(X)''' — [[Средняя непрерывной случайной величины|средняя]] — математическое ожидание;
 
'''M(X)''' — [[Средняя непрерывной случайной величины|средняя]] — математическое ожидание;
Строка 23: Строка 23:
 
'''σ(X)''' — [[Среднеквадратическое отклонение  непрерывной случайной величины|среднеквадратическое отклонение]].
 
'''σ(X)''' — [[Среднеквадратическое отклонение  непрерывной случайной величины|среднеквадратическое отклонение]].
  
−
Параметр '''γ''' равен:  
+
Параметр '''y<sub>0</sub>''' равен:  
  
 
[[файл:КВА00.png]]
 
[[файл:КВА00.png]]
Строка 32: Строка 32:
 
==== График ====
 
==== График ====
 
[[файл:КВА31.png]]
 
[[файл:КВА31.png]]
−
*При '''α=0''' квадратичное распределение становится [[Равномерное распределение|равномерным]].  
+
*При '''k=0''' квадратичное распределение становится [[Равномерное распределение|равномерным]].  
 
=== Интегральная функция ===
 
=== Интегральная функция ===
 
==== Формулы ====
 
==== Формулы ====

Текущая версия на 10:08, 5 мая 2023

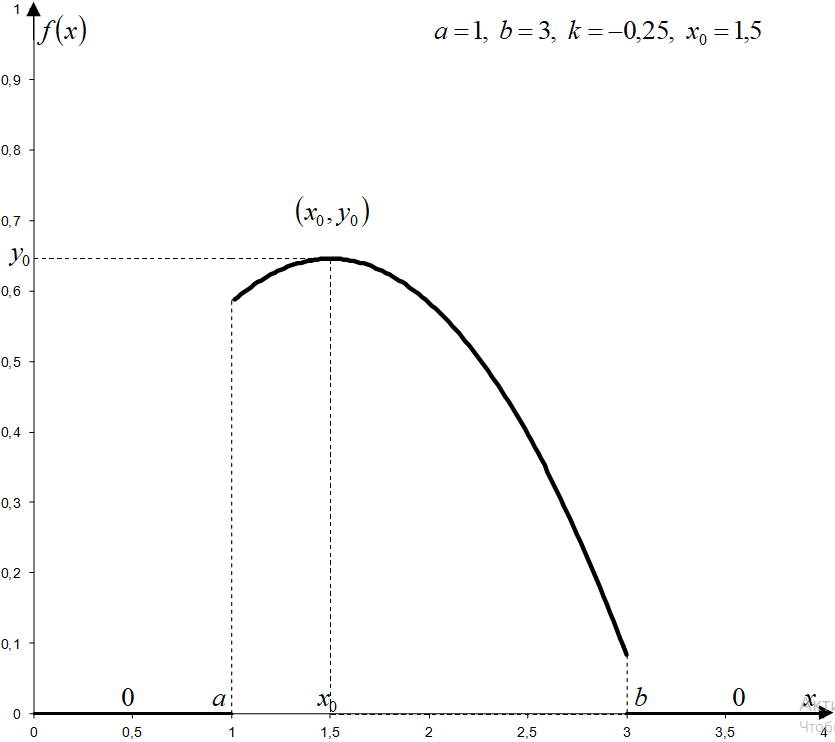
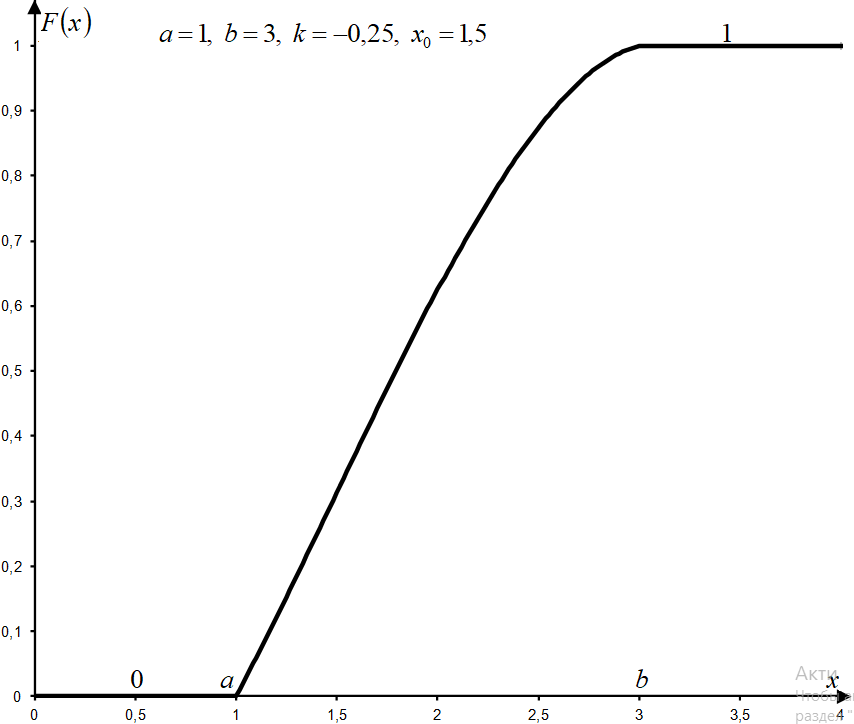
Квадратичное распределение — это распределение непрерывной случайной величины на отрезке с квадратичной плотностью распределения вероятности. График плотности вероятности является частью параболы, с положительными ординатами.

Обозначения

X — случайная величина;

fX(x) — дифференциальная функция распределения — функция плотности вероятности;

FX(x) — интегральная функция распределения — функция вероятности;

a — нижняя граница отрезка;

b — верхняя граница отрезка;

k — коэффициент параболы;

x0 — абсцисса вершины параболы;

y0 — ордината вершины параболы;

M(X) — средняя — математическое ожидание;

D(X) — дисперсия;

σ(X) — среднеквадратическое отклонение.

Параметр y0 равен:

КВА00.png

Функции распределения:

Дифференциальная функция

Формулы

КВА01.png

График

КВА31.png

Интегральная функция

Формулы

КВА02.png

График

КВА32.png

Характеристики:

КВА10.png

Вывод формул:

Математическое ожидание

КВА20.png

Дисперсия

КВА21.png

КВА22.png

Другие распределения:

Ссылки

Источник — «http://megapedia.wiki/w/index.php?title=Квадратичное_распределение&oldid=115497»