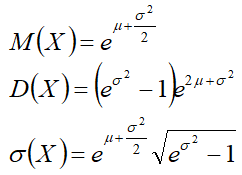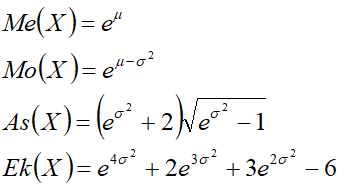Логнормальное распределение — различия между версиями
(начало) |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 28: | Строка 28: | ||
== Функции распределения: == | == Функции распределения: == | ||
=== Дифференциальная функция === | === Дифференциальная функция === | ||
| + | ==== Формулы ==== | ||
[[файл:ЛОГН01.png]] | [[файл:ЛОГН01.png]] | ||
| + | ==== Графики ==== | ||
| + | [[файл:ЛОГН31.png]] | ||
=== Интегральная функция === | === Интегральная функция === | ||
| + | ==== Формулы ==== | ||
[[файл:ЛОГН02.png]] | [[файл:ЛОГН02.png]] | ||
| − | == | + | ==== Графики ==== |
| + | [[файл:ЛОГН32.png]] | ||
| + | == Характеристики: == | ||
[[файл:ЛОГН10.png]] | [[файл:ЛОГН10.png]] | ||
| − | |||
[[файл:ЛОГН11.png]] | [[файл:ЛОГН11.png]] | ||
== [[Распределения вероятностей|Другие распределения:]] == | == [[Распределения вероятностей|Другие распределения:]] == | ||
Текущая версия на 08:11, 21 октября 2024
Логнормальное распределение — это двухпараметрическое распределение непрерывной случайной величины, в котором логарифм распределён нормально.
Содержание
Обозначения[править]
X — случайная величина;
U — стандартизованная случайная величина;
fX(x) — дифференциальная функция распределения — функция плотности вероятности;
FX(x) — интегральная функция распределения — функция вероятности;
φU(u) — дифференциальная функция распределения стандартизованной случайной величины;
ΦU(u) — интегральная функция распределения стандартизованной случайной величины;
M(X)=μ — средняя — математическое ожидание;
D(X) — дисперсия;
σ(X)=σ — среднеквадратическое отклонение;
Me(X) — медиана;
Mo(X) — мода;
As(X) — коэффициент асимметрии;
Ek(X) — коэффициент эксцесса.
Функции распределения:[править]
Дифференциальная функция[править]
Формулы[править]
Графики[править]
Интегральная функция[править]
Формулы[править]
Графики[править]
Характеристики:[править]
Другие распределения:[править]
Распределения ДСВ:
- распределение Бернулли;
- биномиальное распределение;
- геометрическое распределение;
- гипергеометрическое распределение;
- дискретное равномерное распределение;
- распределение Пуассона;
Распределения НСВ:
- бета-распределение;
- распределение Вейбулла;
- гамма-распределение;
- квадратичное распределение;
- распределение Коши;
- распределение Лапласа;
- линейное распределение;
- логистическое распределение;
- логнормальное распределение;
- нормальное распределение;
- распределение Парето;
- показательное распределение;
- равномерное распределение;
- распределение Рэлея;
- распределение Сосновского;
- распределение Стьюдента;
- распределение Фишера-Снедекора;
- распределение Хи-квадрат;
- экспоненциальное распределение;
- Эль-распределение.
Ссылки[править]
- Википедия. Логнормальное распределение.
- https://ru.wikipedia.org/wiki/Логнормальное_распределение
- https://math.fandom.com/ru/wiki/Логнормальное_распределение
- Участник:Logic-samara