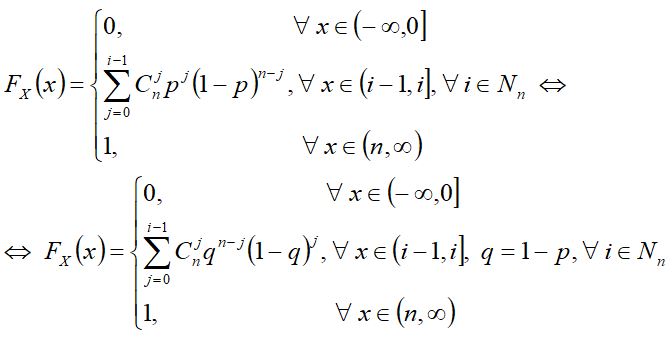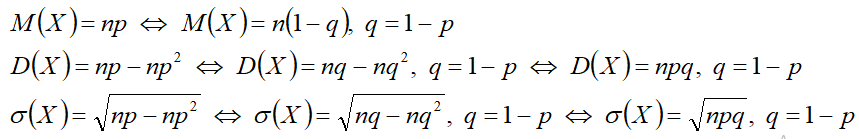Биномиальное распределение — различия между версиями
| Строка 24: | Строка 24: | ||
'''σ(X)''' — [[Среднеквадратическое отклонение дискретной случайной величины|среднеквадратическое отклонение]]; | '''σ(X)''' — [[Среднеквадратическое отклонение дискретной случайной величины|среднеквадратическое отклонение]]; | ||
| + | |||
| + | '''Me(X)''' — [[Медиана дискретной случайной величины|медиана]]; | ||
'''Mo(X)''' — [[Мода дискретной случайной величины|мода]]; | '''Mo(X)''' — [[Мода дискретной случайной величины|мода]]; | ||
Версия 11:59, 6 апреля 2023
Биномиальное распределение — это распределение дискретной случайной величины, равной числу наступлений одного события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p.
Содержание
Обозначения
X — случайная величина;
n — параметр распределения — число испытаний;
p — вероятность наступления события в одном испытании;
q — вероятность не наступления события в одном испытании, q=1-p;
N — множество натуральных чисел;
Nn — множество натуральных чисел от 1 до n;
Cmn — биномиальный коэффициент;
pX(x) — функция вероятности X=x;
FX(x) — интегральная функция распределения — функция вероятности X<x;
M(X) — средняя — математическое ожидание;
D(X) — дисперсия;
σ(X) — среднеквадратическое отклонение;
Me(X) — медиана;
Mo(X) — мода;
As(X) — коэффициент асимметрии;
Ek(X) — коэффициент эксцесса.
Функции распределения:
Функция вероятности
Интегральная функция
- Биномиальное распределение при n=1 является распределением Бернулли.
Формулы:
Вывод формул:
Математическое ожидание
Дисперсия
Другие распределения:
Распределения ДСВ:
- распределение Бернулли;
- биномиальное распределение;
- геометрическое распределение;
- гипергеометрическое распределение;
- дискретное равномерное распределение;
- распределение Пуассона;
Распределения НСВ:
- бета-распределение;
- распределение Вейбулла;
- гамма-распределение;
- квадратичное распределение;
- распределение Коши;
- распределение Лапласа;
- линейное распределение;
- логистическое распределение;
- логнормальное распределение;
- нормальное распределение;
- распределение Парето;
- показательное распределение;
- равномерное распределение;
- распределение Рэлея;
- распределение Сосновского;
- распределение Стьюдента;
- распределение Фишера-Снедекора;
- распределение Хи-квадрат;
- экспоненциальное распределение;
- Эль-распределение.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.511.
- Википедия. Биномиальное распределение.
- https://ru.wikipedia.org/wiki/Биномиальное_распределение
- Участник:Logic-samara