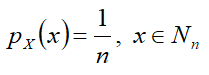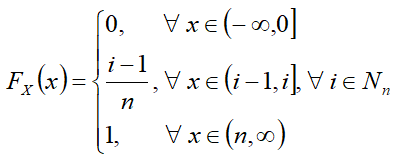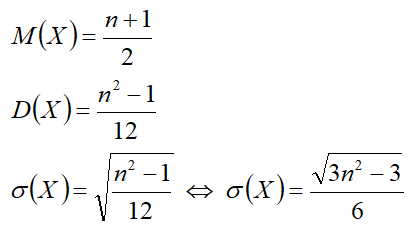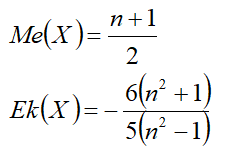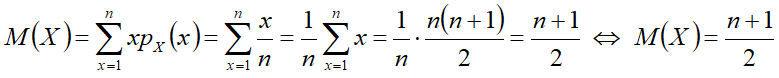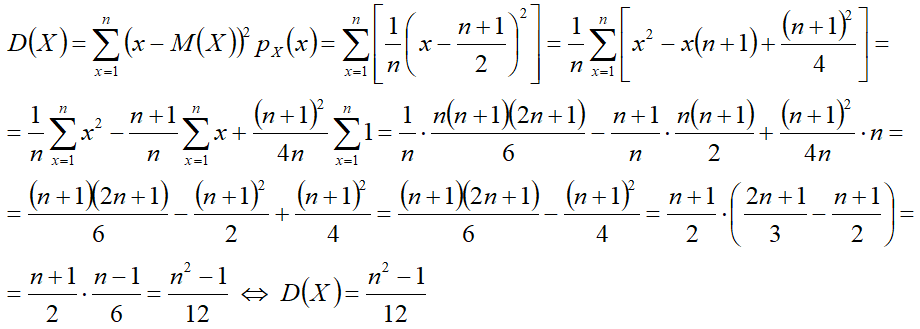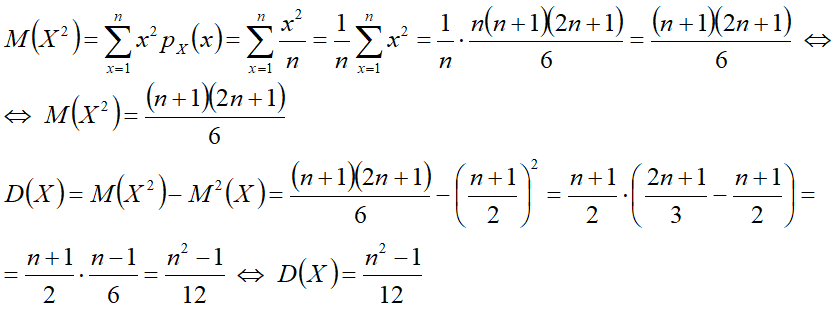Дискретное равномерное распределение

Дискретное равномерное распределение — распределение дискретной случайной величины на конечном множестве значений с постоянной вероятностью события.

Обозначения

X — случайная величина;

n — параметр распределения — число значений;

p — вероятность наступления события в одном испытании, p=1/n;

N_n — множество натуральных чисел от 1 до n;

p_X(x) — функция вероятности P(X=x);

F_X(x) — интегральная функция распределения — функция вероятности P(X<x);

M(X) — средняя — математическое ожидание;

D(X) — дисперсия;

σ(X) — среднеквадратическое отклонение;

Me(X) — медиана;

As(X) — коэффициент асимметрии;

Ek(X) — коэффициент эксцесса.

• Для простоты, рассмотрим случай когда конечное множество из n значений является множеством натуральных чисел N_n, т.е. множеством натуральных чисел от 1 до n.

Функции распределения:

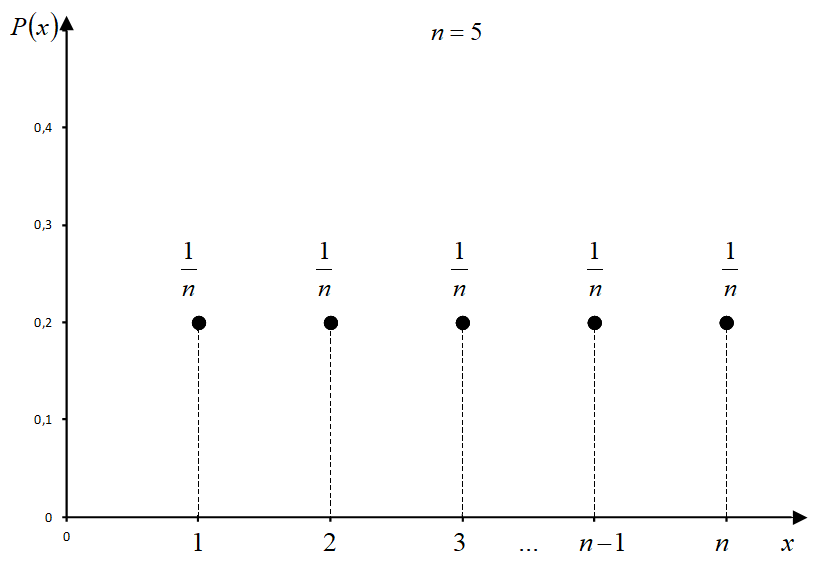
Функция вероятности

Формулы

График

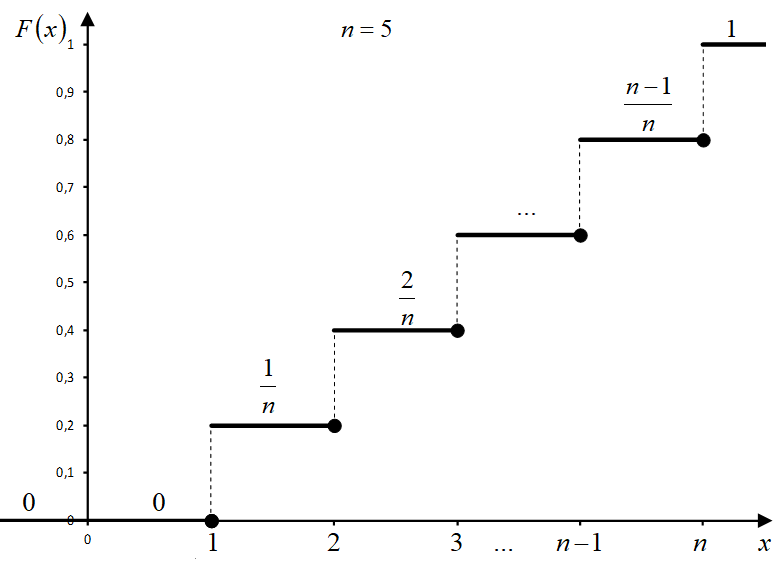
Интегральная функция

Формулы

График

Характеристики

• Формула медианы верна только для нечётных n, для чётных n медиана не существует по определению и формула носит условный характер.
• У дискретного равномерного распределения все значения случайной величины являются модальными по определению.

Вывод формул

Математическое ожидание

Дисперсия

1-й способ

2-й способ

Другие распределения:

Распределения ДСВ:

• распределение Бернулли;
• биномиальное распределение;
• геометрическое распределение;
• гипергеометрическое распределение;
• дискретное равномерное распределение;
• распределение Пуассона;

Распределения НСВ:

• бета-распределение;
• распределение Вейбулла;
• гамма-распределение;
• квадратичное распределение;
• распределение Коши;
• распределение Лапласа;
• линейное распределение;
• логистическое распределение;
• логнормальное распределение;
• нормальное распределение;
• распределение Парето;
• показательное распределение;
• равномерное распределение;
• распределение Рэлея;
• распределение Сосновского;
• распределение Стьюдента;
• распределение Фишера-Снедекора;
• распределение Хи-квадрат;
• экспоненциальное распределение;
• Эль-распределение.

Ссылки

• Участник:Logic-samara