Гипотеза о вероятности равной числу — различия между версиями
(начало) |
м |
||
| (не показано 5 промежуточных версий этого же участника) | |||
| Строка 21: | Строка 21: | ||
'''Φ(u)''' — интегральная функция распределения стандартизованной случайной величины. | '''Φ(u)''' — интегральная функция распределения стандартизованной случайной величины. | ||
== Гипотезы о вероятности: == | == Гипотезы о вероятности: == | ||
| + | <!--[[файл:СТН00.png]]--> | ||
| + | |||
[[файл:СТН00.JPG]] — статистика, распределённая по нормальному закону '''N(0;1)'''. | [[файл:СТН00.JPG]] — статистика, распределённая по нормальному закону '''N(0;1)'''. | ||
=== Пример 1 === | === Пример 1 === | ||
| Строка 27: | Строка 29: | ||
'''H<sub>1</sub>:p≠p<sub>0</sub>'''; | '''H<sub>1</sub>:p≠p<sub>0</sub>'''; | ||
| − | [[файл: | + | [[файл:СТН02.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''. |
=== Пример 2 === | === Пример 2 === | ||
| − | '''H<sub>0</sub>: | + | '''H<sub>0</sub>:p=p<sub>0</sub>'''; |
'''H<sub>1</sub>:p>p<sub>0</sub>'''; | '''H<sub>1</sub>:p>p<sub>0</sub>'''; | ||
| − | [[файл: | + | [[файл:СТН03.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''. |
=== Пример 3 === | === Пример 3 === | ||
| − | '''H<sub>0</sub>: | + | '''H<sub>0</sub>:p=p<sub>0</sub>'''; |
'''H<sub>1</sub>:p<p<sub>0</sub>'''; | '''H<sub>1</sub>:p<p<sub>0</sub>'''; | ||
| − | [[файл:СТН04. | + | [[файл:СТН04.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''. |
== [[Гипотезы|Другие гипотезы:]] == | == [[Гипотезы|Другие гипотезы:]] == | ||
{{Список Гип}} | {{Список Гип}} | ||
| Строка 45: | Строка 47: | ||
*Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2004, стр.369. | *Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2004, стр.369. | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
| − | [[Категория:Математическая статистика]] | + | [[Категория:Математика]][[Категория:Математическая статистика]] |
Текущая версия на 10:16, 7 апреля 2025
Гипотеза о вероятности равной числу для нормально распределённой случайной величины использует статистику, имеющую стандартизованное распределение, N(0;1).
Содержание
Обозначения
n — число значений в выборке;
m — частота значений альтернативного признака среди n значений в выборке;
p0 — положительная дробь;
p — вероятность значений альтернативного признака;
np — математическое ожидание частоты альтернативного признака;
σ — среднеквадратическое отклонение альтернативного признака;
D=np(1-p) — дисперсия альтернативного признака;
α — уровень значимости — вероятность ошибки 1-го рода;
u — переменная стандартизованной случайной величины;
Φ(u) — интегральная функция распределения стандартизованной случайной величины.
Гипотезы о вероятности:
— статистика, распределённая по нормальному закону N(0;1).
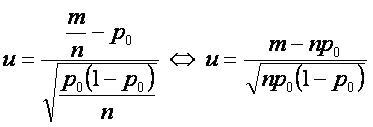
Пример 1
H0:p=p0;
H1:p≠p0;
— критерий отклонения гипотезы H0.
Пример 2
H0:p=p0;
H1:p>p0;
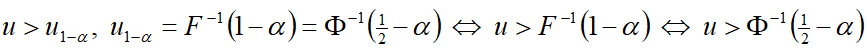— критерий отклонения гипотезы H0.
Пример 3
H0:p=p0;
H1:p<p0;
— критерий отклонения гипотезы H0.
Другие гипотезы:
- Гипотеза о средней равной числу при известной дисперсии;
- Гипотеза о средней равной числу при неизвестной дисперсии;
- Гипотеза о дисперсии равной числу при известной средней;
- Гипотеза о дисперсии равной числу при неизвестной средней;
- Гипотеза о равенстве дисперсий;
- Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий;
- Гипотеза о равенстве нескольких дисперсий;
- Гипотеза о равенстве средних при известных дисперсиях;
- Гипотеза о равенстве разности средних числу при известных дисперсиях;
- Гипотеза о равенстве средних при неизвестных равных дисперсиях;
- Гипотеза о равенстве средних при неизвестных дисперсиях;
- Гипотеза о вероятности равной числу;
- Гипотеза о равенстве вероятностей;
- Гипотеза о нормальном законе распределения;
- Гипотеза об отсутствии линейной корреляционной связи;
- Гипотеза о коэффициенте линейного уравнения регрессии равном нулю;
- Гипотеза о коэффициенте линейного уравнения множественной регрессии равном нулю;
- Гипотеза о значимости линейного уравнения регрессии;
- Гипотеза о значимости линейного уравнения множественной регрессии;
- Гипотеза о коэффициенте корреляции равном числу;
- Гипотеза о коэффициенте корреляции равном нулю;
- Гипотеза о равенстве коэффициентов корреляции.
Ссылки
- Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2004, стр.369.
- Участник:Logic-samara
