Гипотеза о дисперсии равной числу при неизвестной средней

Гипотеза о дисперсии равной числу при неизвестной средней для нормально распределённой случайной величины использует статистику, имеющую X²-распределение.

Обозначения

n — число значений в выборке;

D₀ — положительное число;

D_Г — дисперсия генеральной совокупности;

= — средняя в выборке X, ;

σ_в=σ — среднеквадратическое отклонение выборки, ;

s — исправленное среднеквадратическое отклонение выборки, ;

α — уровень значимости — вероятность ошибки 1-го рода;

γ=1-α — коэффициент доверия;

X² — переменная X²-распределения;

k — число степеней свободы, k=n-1;

F_X²(X²,k) — интегральная функция X²-распределения.

Гипотезы о дисперсии:

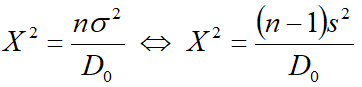— статистика, имеющая X²-распределение.

Пример 1

H₀:D_Г=D₀;

H₁:D_Г≠D₀;

— критерий отклонения гипотезы H₀.

Пример 2

H₀:D_Г=D₀;

H₁:D_Г>D₀;

— критерий отклонения гипотезы H₀.

Пример 3

H₀:D_Г=D₀;

H₁:D_Г<D₀;

— критерий отклонения гипотезы H₀.

Другие гипотезы:

1. Гипотеза о средней равной числу при известной дисперсии;
2. Гипотеза о средней равной числу при неизвестной дисперсии;
3. Гипотеза о дисперсии равной числу при известной средней;
4. Гипотеза о дисперсии равной числу при неизвестной средней;
5. Гипотеза о равенстве дисперсий;
6. Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий;
7. Гипотеза о равенстве нескольких дисперсий;
8. Гипотеза о равенстве средних при известных дисперсиях;
9. Гипотеза о равенстве разности средних числу при известных дисперсиях;
10. Гипотеза о равенстве средних при неизвестных равных дисперсиях;
11. Гипотеза о равенстве средних при неизвестных дисперсиях;
12. Гипотеза о вероятности равной числу;
13. Гипотеза о равенстве вероятностей;
14. Гипотеза о нормальном законе распределения;
15. Гипотеза об отсутствии линейной корреляционной связи;
16. Гипотеза о коэффициенте линейного уравнения регрессии равном нулю;
17. Гипотеза о коэффициенте линейного уравнения множественной регрессии равном нулю;
18. Гипотеза о значимости линейного уравнения регрессии;
19. Гипотеза о значимости линейного уравнения множественной регрессии;
20. Гипотеза о коэффициенте корреляции равном числу;
21. Гипотеза о коэффициенте корреляции равном нулю;
22. Гипотеза о равенстве коэффициентов корреляции.

Ссылки

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.561.