Гипотеза о значимости линейного уравнения множественной регрессии — различия между версиями

Материал из Мегапедии
Перейти к: навигация, поиск
(начало)
 
м
 
(не показаны 2 промежуточные версии этого же участника)
Строка 1: Строка 1:
−
'''Гипотеза о значимости линейного уравнения множественной регрессии''' — гипотеза о равенстве нулю всех [[Коэффициент уравнения множественной регрессии|коэффициентов регрессии]] при независимых переменных.
+
'''Гипотеза о значимости линейного уравнения множественной регрессии''' — гипотеза о равенстве нулю всех [[Коэффициент множественной регрессии|коэффициентов регрессии]] при независимых переменных.
  
 
== Обозначения ==
 
== Обозначения ==
Строка 6: Строка 6:
 
'''k''' — число независимых переменных;
 
'''k''' — число независимых переменных;
  
−
<math>y = b_0 + b_1x_1 + b_2x_2 + \ldots + b_kx_k</math> — линейное уравнение множественной регрессии;
+
'''y = b<sub>0</sub> + b<sub>1</sub>x<sub>1</sub> + b<sub>2</sub>x<sub>2</sub> + ... + b<sub>k</sub>x<sub>k</sub>''' — линейное уравнение множественной регрессии;
  
 
[[файл:MXnk1.png]] — [[матрица]] значений независимых переменных в выборке;
 
[[файл:MXnk1.png]] — [[матрица]] значений независимых переменных в выборке;
  
−
[[файл:Vyn.png]] — значения зависимой переменной; [[файл:Vbk.png]] — [[Коэффициент уравнения множественной регрессии|коэффициенты уравнения регрессии]];
+
[[файл:Vyn.png]] — значения зависимой переменной; [[файл:Vbk.png]] — [[Коэффициент множественной регрессии|коэффициенты уравнения регрессии]];
  
 
'''n-k-1''' — число степеней свободы;
 
'''n-k-1''' — число степеней свободы;
Строка 23: Строка 23:
  
 
=== Пример 1 ===
 
=== Пример 1 ===
−
<math>H_0: \text{Ɐ j ϵ } N_k , b_j=0;</math>
+
'''H_0: Ɐ j ϵ N<sub>k</sub>, b<sub>j</sub>=0;'''
  
−
<math>H_1: \text{ⱻ j ϵ } N_k , \text{т.ч. } b_j \text{≠} 0;</math>
+
'''H_1: ⱻ j ϵ N<sub>k</sub>, т.ч. b<sub>j</sub>≠0;'''
  
 
[[файл:СТФ22.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''.
 
[[файл:СТФ22.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''.

Текущая версия на 04:42, 21 марта 2025

Гипотеза о значимости линейного уравнения множественной регрессии — гипотеза о равенстве нулю всех коэффициентов регрессии при независимых переменных.

Обозначения

n — число значений в выборке;

k — число независимых переменных;

y = b0 + b1x1 + b2x2 + ... + bkxk — линейное уравнение множественной регрессии;

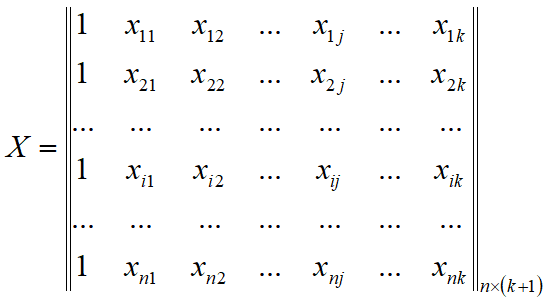MXnk1.png — матрица значений независимых переменных в выборке;

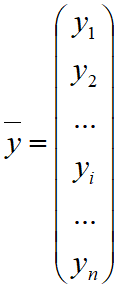Vyn.png — значения зависимой переменной; 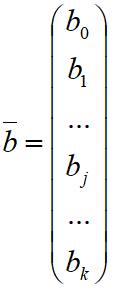Vbk.png — коэффициенты уравнения регрессии;

n-k-1 — число степеней свободы;

Nk — множество натуральных чисел j, 1≤j≤k.

FF(F,k1,k2) — интегральная функция распределения Фишера-Снедекора.

Fтабл(αтабл,k,n-k-1)=FF-1(1-αтабл,k,n-k-1) — табличное значение для F.

Гипотеза о значимости уравнения множественной регрессии

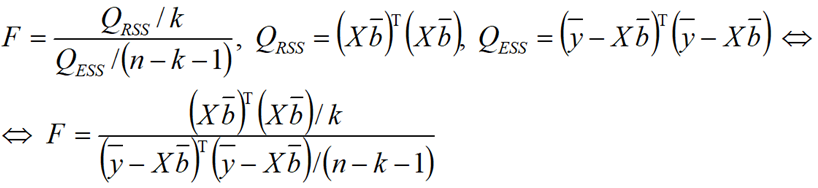СТФ21.png — статистика, имеющая распределение Фишера-Снедекора

Пример 1

H_0: Ɐ j ϵ Nk, bj=0;

H_1: ⱻ j ϵ Nk, т.ч. bj≠0;

СТФ22.png — критерий отклонения гипотезы H0.

Другие гипотезы

Ссылки

Источник — «http://megapedia.wiki/w/index.php?title=Гипотеза_о_значимости_линейного_уравнения_множественной_регрессии&oldid=131164»