Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий — различия между версиями

Материал из Мегапедии
Перейти к: навигация, поиск
(начало)
 
м
Строка 2: Строка 2:
  
 
== Обозначения ==
 
== Обозначения ==
−
'''k''' — число групп-выборок;
+
'''<big>k</big>''' — число групп-выборок;
  
−
'''n<sub>i</sub>''' — число значений в выборке '''i'''-группы cлучайной величины X;
+
'''<big>n<sub>i</sub></big>''' — число значений в выборке '''i'''-группы cлучайной величины X;
  
−
'''n''' — число значений во всех выборках X, <math> n = \sum\limits_{i=1}^{k}{n_i}</math>;
+
'''<big>n</big>''' — число значений во всех выборках X, <math> n = \sum\limits_{i=1}^{k}{n_i}</math>;
  
 
<math>\bar x</math> — общая средняя всех выборок X, <math> \bar x = \frac{1}{n} \sum\limits_{i=1}^{k}{\sum\limits_{j=1}^{n_i}{x_{ij}}}</math>;
 
<math>\bar x</math> — общая средняя всех выборок X, <math> \bar x = \frac{1}{n} \sum\limits_{i=1}^{k}{\sum\limits_{j=1}^{n_i}{x_{ij}}}</math>;
Строка 12: Строка 12:
 
<math>\bar x_i</math> — средняя в выборке '''i'''-группы X, <math> \bar x_i = \frac{1}{n_i} \sum\limits_{j=1}^{n_i}{x_{ij}}</math>;
 
<math>\bar x_i</math> — средняя в выборке '''i'''-группы X, <math> \bar x_i = \frac{1}{n_i} \sum\limits_{j=1}^{n_i}{x_{ij}}</math>;
  
−
<math>D_{\text{мгр}}</math> — дисперсия межгрупповая в генеральной совокупности;
+
'''<big>D<sub>мгр</sub></big>''' — дисперсия межгрупповая в генеральной совокупности;
  
−
<math>D_{\text{вгр}}</math> — дисперсия внутригрупповая в генеральной совокупности;
+
'''<big>D<sub>вгр</sub></big>''' — дисперсия внутригрупповая в генеральной совокупности;
  
−
'''α''' — уровень значимости — вероятность ошибки 1-го рода;
+
'''<big>α</big>''' — уровень значимости — вероятность ошибки 1-го рода;
  
−
'''γ=1-α''' — [[Доверительный интервал средней при неизвестной дисперсии|коэффициент доверия]];
+
'''<big>γ=1-α</big>''' — [[Доверительный интервал средней при неизвестной дисперсии|коэффициент доверия]];
  
−
'''F''' — переменная [[Распределение Фишера-Снедекора|распределения Фишера-Снедекора]];
+
'''<big>F</big>''' — переменная [[Распределение Фишера-Снедекора|распределения Фишера-Снедекора]];
  
−
'''k<sub>мгр</sub>''' — число степеней свободы для межгрупповой дисперсии, '''k<sub>x</sub>=k-1''';
+
'''<big>k<sub>мгр</sub></big>''' — число степеней свободы для межгрупповой дисперсии, '''k<sub>x</sub>=k-1''';
  
−
'''k<sub>вгр</sub>''' — число степеней свободы для средней внутригрупповых дисперсий, ''' k<sub>вгр</sub>=n-k''';
+
'''<big>k<sub>вгр</sub></big>''' — число степеней свободы для средней внутригрупповых дисперсий, ''' k<sub>вгр</sub>=n-k''';
  
−
'''F<sub>F</sub>(t,k-1,n-k)''' — интегральная функция распределения Фишера-Снедекора.
+
'''<big>F<sub>F</sub>(t,k-1,n-k)</big>''' — интегральная функция распределения Фишера-Снедекора.
  
−
'''F<sub>табл</sub>(α<sub>табл</sub>,k<sub>x</sub>,k<sub>y</sub>)=F<sub>F</sub><sup>-1</sup>(1-α<sub>табл</sub>,k<sub>x</sub>,k<sub>y</sub>)''' — выражение '''Fтабл''' через интегральную функцию Фишера-Снедекора;
+
'''<big>F<sub>табл</sub>(α<sub>табл</sub>,k<sub>x</sub>,k<sub>y</sub>)=F<sub>F</sub><sup>-1</sup>(1-α<sub>табл</sub>,k<sub>x</sub>,k<sub>y</sub>)</big>''' — выражение '''Fтабл''' через интегральную функцию Фишера-Снедекора;
  
−
'''α<sub>табл</sub>(F<sub>табл</sub>,k<sub>x</sub>,k<sub>y</sub>)=P(F>F<sub>1-α<sub>табл</sub>,k<sub>x</sub>,k<sub>y</sub></sub>)''' — соответствие веороятности для табличного значения '''Fтабл'''.
+
'''<big>α<sub>табл</sub>(F<sub>табл</sub>,k<sub>x</sub>,k<sub>y</sub>)=P(F>F<sub>1-α<sub>табл</sub>,k<sub>x</sub>,k<sub>y</sub></sub>)</big>''' — соответствие веороятности для табличного значения '''Fтабл'''.
 
== Гипотезы о дисперсиях ==
 
== Гипотезы о дисперсиях ==
 
[[файл:СТФ31.png]] — статистика, имеющая [[распределение Фишера-Снедекора]].
 
[[файл:СТФ31.png]] — статистика, имеющая [[распределение Фишера-Снедекора]].
 
=== Пример 1 ===
 
=== Пример 1 ===
−
<math>H_0: D_{\text{мгр}} = D_{\text{вгр}};</math>
+
'''<big>H<sub>0</sub>:D<sub>мгр</sub>=D<sub>вгр</sub>;</big>'''
  
−
<math>H_1: D_{\text{мгр}} > D_{\text{вгр}};</math>
+
'''<big>H<sub>1</sub>:D<sub>мгр</sub>>D<sub>вгр</sub>;</big>'''
  
 
[[Файл:СТФ32.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''.
 
[[Файл:СТФ32.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''.
 
=== Пример 2 ===
 
=== Пример 2 ===
−
<math>H_0: D_{\text{мгр}} = D_{\text{вгр}};</math>
+
'''<big>H<sub>0</sub>:D<sub>мгр</sub>=D<sub>вгр</sub>;</big>'''
  
−
<math>H_1: D_{\text{мгр}} \text{ ≠ } D_{\text{вгр}};</math>
+
'''<big>H<sub>1</sub>:D<sub>мгр</sub>≠D<sub>вгр</sub>;</big>'''
  
 
[[Файл:СТФ33.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''.
 
[[Файл:СТФ33.png]] — критерий отклонения гипотезы '''H<sub>0</sub>'''.

Версия 09:05, 21 февраля 2025

Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий — гипотеза о том, что дисперсия между группами и средняя дисперсия групп равны.

Обозначения

k — число групп-выборок;

ni — число значений в выборке i-группы cлучайной величины X;

n — число значений во всех выборках X, <math> n = \sum\limits_{i=1}^{k}{n_i}</math>;

<math>\bar x</math> — общая средняя всех выборок X, <math> \bar x = \frac{1}{n} \sum\limits_{i=1}^{k}{\sum\limits_{j=1}^{n_i}{x_{ij}}}</math>;

<math>\bar x_i</math> — средняя в выборке i-группы X, <math> \bar x_i = \frac{1}{n_i} \sum\limits_{j=1}^{n_i}{x_{ij}}</math>;

Dмгр — дисперсия межгрупповая в генеральной совокупности;

Dвгр — дисперсия внутригрупповая в генеральной совокупности;

α — уровень значимости — вероятность ошибки 1-го рода;

γ=1-α — коэффициент доверия;

F — переменная распределения Фишера-Снедекора;

kмгр — число степеней свободы для межгрупповой дисперсии, kx=k-1;

kвгр — число степеней свободы для средней внутригрупповых дисперсий, kвгр=n-k;

FF(t,k-1,n-k) — интегральная функция распределения Фишера-Снедекора.

Fтабл(αтабл,kx,ky)=FF-1(1-αтабл,kx,ky) — выражение Fтабл через интегральную функцию Фишера-Снедекора;

αтабл(Fтабл,kx,ky)=P(F>F1-αтабл,kx,ky) — соответствие веороятности для табличного значения Fтабл.

Гипотезы о дисперсиях

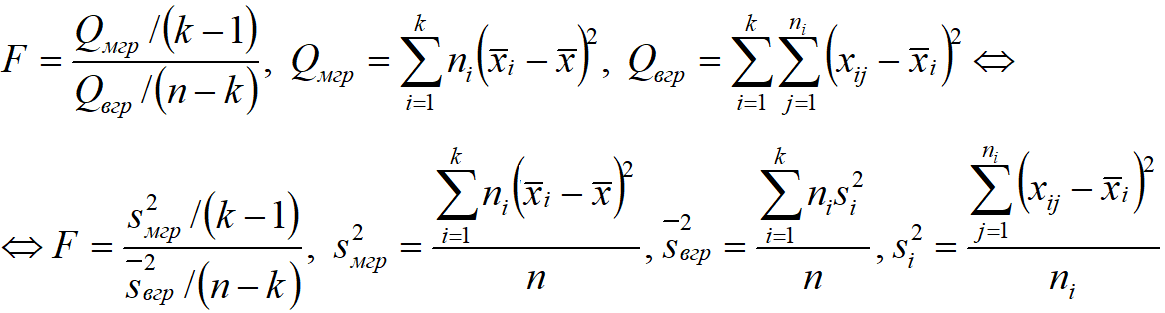СТФ31.png — статистика, имеющая распределение Фишера-Снедекора.

Пример 1

H0:Dмгр=Dвгр;

H1:Dмгр>Dвгр;

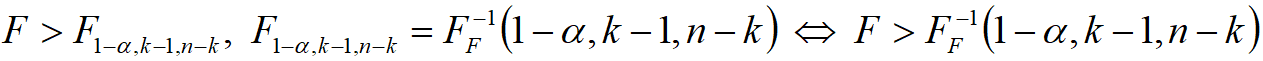СТФ32.png — критерий отклонения гипотезы H0.

Пример 2

H0:Dмгр=Dвгр;

H1:Dмгр≠Dвгр;

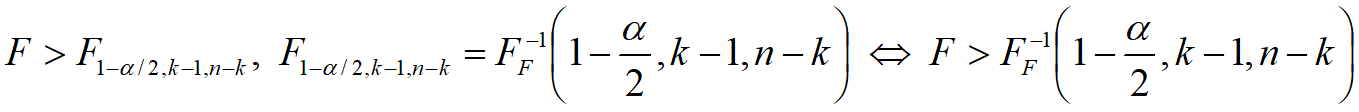СТФ33.png — критерий отклонения гипотезы H0.

Другие гипотезы:


Ссылки

Источник — «http://megapedia.wiki/w/index.php?title=Гипотеза_о_равенстве_межгрупповой_и_внутригрупповой_дисперсий&oldid=131000»