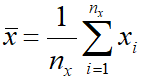Гипотеза о равенстве средних при неизвестных дисперсиях — различия между версиями
м |
м |
||
| Строка 4: | Строка 4: | ||
== Обозначения == | == Обозначения == | ||
| − | '''n<sub>x</sub>''' — число значений в выборке X; | + | '''<big>n<sub>x</sub></big>''' — число значений в выборке X; |
| − | '''n<sub>y</sub>''' — число значений в выборке Y; | + | '''<big>n<sub>y</sub></big>''' — число значений в выборке Y; |
| − | '''n''' — число значений в меньшей выборке '''n=min{n<sub>x</sub>,n<sub>y</sub>}'''; | + | '''<big>n</big>''' — число значений в меньшей выборке '''<big>n=min{n<sub>x</sub>,n<sub>y</sub>}</big>'''; |
'''<big>n<sub>x</sub></big>''' — число значений в выборке X; | '''<big>n<sub>x</sub></big>''' — число значений в выборке X; | ||
| Строка 28: | Строка 28: | ||
'''<big>t</big>''' — переменная распределения Стьюдента; | '''<big>t</big>''' — переменная распределения Стьюдента; | ||
| − | '''<big>k</big>''' — число степеней свободы, '''k≈n-1</big>'''; | + | '''<big>k</big>''' — число степеней свободы, '''<big>k≈n-1</big>'''; |
'''<big>F<sub>Ст</sub>(t,k)</big>''' — интегральная функция распределения Стьюдента. | '''<big>F<sub>Ст</sub>(t,k)</big>''' — интегральная функция распределения Стьюдента. | ||
Версия 14:57, 21 февраля 2025
Гипотеза о равенстве средних при неизвестных дисперсиях — гипотеза о том, что при неизвестных неравных дисперсиях, средние двух совокупностей равны.
Для нормально распределённой случайной величины использует статистику, имеющую t-распределение Стьюдента.
Содержание
Обозначения
nx — число значений в выборке X;
ny — число значений в выборке Y;
n — число значений в меньшей выборке n=min{nx,ny};
nx — число значений в выборке X;
ny — число значений в выборке Y;
=
— средняя в выборке X, 
;
=
— средняя в выборке Y, 
;
sx — среднеквадратическое отклонение в выборке X, 
;
sy — среднеквадратическое отклонение в выборке Y, 
;
α — уровень значимости — вероятность ошибки 1-го рода;
γ=1-α — коэффициент доверия;
t — переменная распределения Стьюдента;
k — число степеней свободы, k≈n-1;
FСт(t,k) — интегральная функция распределения Стьюдента.
tтабл=FСт-1(1-αтабл/2,k) — табличное значение для t;
FСт_табл(αтабл,k)=P(|t|>t1-αтабл,k) — табличное значение FСт_табл.
Гипотезы о средней
— статистика, имеющая распределение Стьюдента.
Пример 1
H0:
=
;
H1:≠;
— критерий отклонения гипотезы H0.
Пример 2
H0:≤;
H1:>;
— критерий отклонения гипотезы H0.
- Заметим, что t1-α,n-1=-tα,n-1.
Пример 3
H0:≥;
H1:<;
— критерий отклонения гипотезы H0.
- Заметим, что tα,n-1=-t1-α,n-1.
Пример 4
H0:≠;
H1:=;
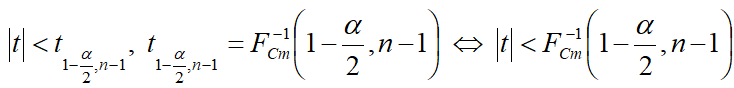— критерий отклонения гипотезы H0.
Другие гипотезы:
- Гипотеза о средней равной числу при известной дисперсии;
- Гипотеза о средней равной числу при неизвестной дисперсии;
- Гипотеза о дисперсии равной числу при известной средней;
- Гипотеза о дисперсии равной числу при неизвестной средней;
- Гипотеза о равенстве дисперсий;
- Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий;
- Гипотеза о равенстве нескольких дисперсий;
- Гипотеза о равенстве средних при известных дисперсиях;
- Гипотеза о равенстве разности средних числу при известных дисперсиях;
- Гипотеза о равенстве средних при неизвестных равных дисперсиях;
- Гипотеза о равенстве средних при неизвестных дисперсиях;
- Гипотеза о вероятности равной числу;
- Гипотеза о равенстве вероятностей;
- Гипотеза о нормальном законе распределения;
- Гипотеза об отсутствии линейной корреляционной связи;
- Гипотеза о коэффициенте линейного уравнения регрессии равном нулю;
- Гипотеза о коэффициенте линейного уравнения множественной регрессии равном нулю;
- Гипотеза о значимости линейного уравнения регрессии;
- Гипотеза о значимости линейного уравнения множественной регрессии;
- Гипотеза о коэффициенте корреляции равном числу;
- Гипотеза о коэффициенте корреляции равном нулю;
- Гипотеза о равенстве коэффициентов корреляции.
